Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng công thức tính lực đàn hồi và trọng lượng
Cách giải:
+ Thời gian quả cầu đi từ vị trí cao nhất đến VT thấp nhất là 0,15s → T/2 = 0,15 s → T = 0,3 s.
→ Độ giãn của lò xo ở VTCB:
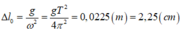
+ Khi con lắc ở vị trí thấp nhất thì: F d h = k . ( ∆ l 0 + a )
Theo đề bài ta có:
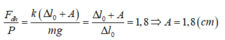

Đáp án B
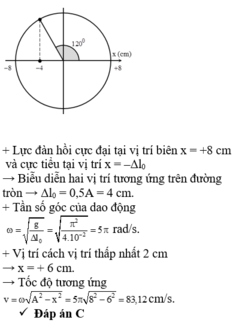
+ Độ biến dạng của lò xo tại vị trí cân bằng 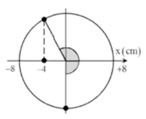
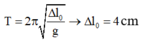
+ Biểu diễn dao động của con lắc tương ứng trên đường tròn.
Lực đàn hồi của lò xo có độ lớn cực tiểu lần đầu tiên khi vật đi qua vị trí lò xo không biến dạng lần đầu, tương ứng với
![]()
→ Từ hình vẽ, ta có
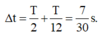

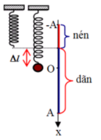


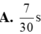
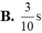
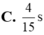


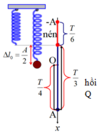
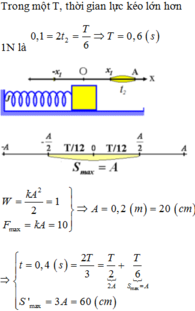
Thời gian quả cầu đi từ vị trí cao nhất (x = -A) đến vị trí thấp nhất (x = A) chính là \(\frac{T}{2} = 0,2 => T = 0,4s.\)
Lực đàn hồi của lò xo khi lò xo ở vị trí thấp nhất chính là \(F_{dhmax} = k(A+\Delta l)\)
\(\frac{F_{max}}{P} = \frac{k(A+\Delta l)}{mg} = \frac{kA+k\Delta l }{mg } = 1+\frac{kA}{mg} =\frac{7}{4}\) (do \(k\Delta l = mg\))
=> \(A = \frac{3g}{4}\frac{m}{k} = \frac{3g}{4}.\frac{T^2}{4\pi^2} =0,03m = 3cm.\)
<3