Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


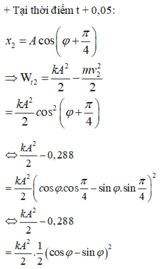


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

Chọn đáp án D
@ Lời giải:
+ Thế năng của vật dao động điều hòa biến thiên tuần hoàn với tần số góc:
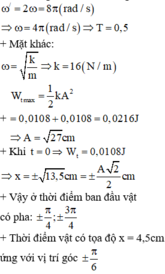
+ Vậy thời điểm vật qua vị trí x = 4,5cm lần đầu tiên là: T 24 = 1 48 s

Đáp án D
Phương pháp: Thế năng đàn hồi : Thế năng đàn hồi :
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: ![]()
Biên độ dao động của con lắc: A = 7,5 - Δl0 = 7,5 - 2,5 = 5cm
Ta có: Δl0< A
Chọn chiều dương hướng xuống
=> Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo hông giãn cũng hông nén: Δl = 0
Thế năng đàn hồi tại vị trí đó: 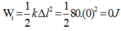

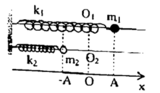
+ Phương trình dao động của hai con lắc lò xo
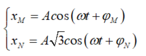
Khoảng cách giữa hai vật nặng của hai con lắc lò xo tại thời điểm t là:
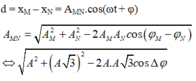
Trong quá trình dao động, độ chênh lệch độ cao lớn nhất của hai vật là A
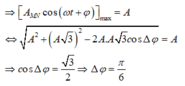
Động năng của con lắc M cực đại W đ m = k A 2 2 = 0 , 12 J khi vật M ở VTCB. Khi đó ta biểu diễn được vị trí của vật N được biểu diễn trên đường tròn lượng giác (M và N lệch pha nhau góc π/6).
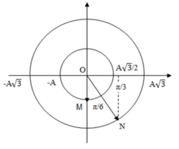
+ Từ đường tròn lượng giác xác định được

Đáp án D

Biên độ: \(A=10cm\)
Tần số góc: \(\omega=10(rad/s)\)
Tại vị trí lò xo bị giãn \(5cm\) thì li độ của vật là: \(x=-10+5=-5cm\)
Vật đang đi lên là chuyển động theo chiều âm.
\(\Rightarrow \cos\varphi=-\dfrac{5}{10}=-0,5\)
\(\Rightarrow \varphi = \dfrac{2\pi}{3}\) (rad) (vì vật chuyển động theo chiều âm nên \(\varphi < 0\) )
PT dao động: \(x=10\cos(10t+\dfrac{2\pi}{3}) (cm)\)
Ở VTCB lò xo giãn 10 cm, như vậy để nó giãn 5cm thì từ VTCB phải đi lên 5cm.
Chiều dương hướng xuống, nên li độ lúc đó phải bằng -5cm.

Phương pháp: Hai vật có cùng li độ khi x1 = x2
Cách giải:
Tần số góc của con lắc lò xo 1 và 2:
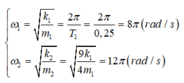
Theo bài ra ta có phương trình dao động của con lắc 1 và 2:
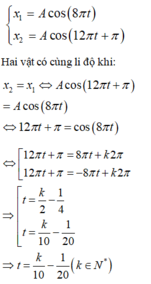
Hai vật có cùng li độ lần thứ 2018 ứng với k = 2018
Đáp án A

Chọn đáp án A
@ Lời giải:
+ Tần số ngoại lực cưỡng bức bằng tần số hệ dao động cưỡng bức.
+ Tốc độ cực đại vmax= ꞷA = 10π.5 = 50π cm/s
ü Chọn đáp án A

Phương pháp: Áp dụng định luật bảo toàn động lượng
Cách giải:
Gọi vận tốc của hệ ngay sau khi va chạm là v. Áp dụng định luật bảo toàn động lượng ta có:

Đáp án A

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
Đáp án C