Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Tần số góc của dao động ω = k m = 10 π rad/s.
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 1 c m
+ Khi vật đang ở vị trí có li độ x = –1 cm → l = l 0 = 40 c m , người ta tiến hành giữ cố định lò xo tại điểm cách điểm cố định 20 cm → lò xo mới tham gia vào dao động có độ cứng k' = 2k = 200 N/m.
+ Năng lượng của con lắc trước khi cố định lò xo: E t = k x 2 = 0 , 01 E d = 1 2 k A 2 − x 2 = 0 , 035 J
→ Năng lượng của hệ sau cố định lò xo đúng bằng tổng động năng và một nửa thế năng của vật trước khi cố định lò xo.
E ' = 0 , 5 k A ' 2 = E d + 0 , 5 E t = 0 , 04 J → A' = 0,02 cm.
→ Lực đàn hồi cực đại F m a x = k ' ( 0 , 5 Δ l 0 + A ' ) = 6 N .
Đáp án B

Chọn đáp án A
Δ l = m g k = T 2 4 π 2 g = 0 , 04 m = 4 c m T h ờ i g i a n t ừ x = 0 → x = + A → x = 0 → x = − A 2 T 4 + T 4 + T 12 = 7 T 12 = 7 30 s là:
Tốc độ trung bình:
v = s t = A + A + 0 , 5 A t = 85 , 7 c m / s

Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hòa
Cách giải :
Vị trí cân bằng lò xo dãn một đoạn ∆ ε , ta có:
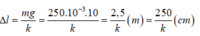
Vật được thả nhẹ từ vị trí lò xo dãn 6,5cm => biên độ dao động: A = 6,5 - 250 k
Vì A < 6,5cm nên dựa vào đáp án ta chọn A = 4cm
![]()
=> Phương trình dao động của vật: x = 4cos(20t) (cm)

Đáp án B
Phương pháp: Sử dụng lí thuyết về lực đàn hồi của con lắc lò xo đặt thẳng đứng
Cách giải:
Ở VTCB lò xo dãn một đoạn ∆ l . Ta có
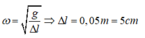
Biên độ dao động A = 5cm
Khi ở vị trí cao nhất, lò xo không biến dạng nên lực đàn hồi của lò xo có độ lớn bằng 0.

Chọn D

+ T = 1s => ω = 2π rad/s.
+ Độ biến dạng của lò xo ở vị trí cân bằng:
![]()
+ Biên độ dao động:
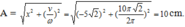
+ Thời điểm t = 0 tương ứng với một gốc lùi Δφ = ωt = 2π.2,5 = 5π trên đường tròn.
+ Lực đàn hồi khi đó có độ lớn:
Fđh = k(Δlo + x) = k(25 + 5√2). 10-2 N.
Kết hợp với Fđhmin = k.(Δlo - A) = k. 15.10-2 = 6N.
+ Từ hai biểu thức trên ta thu được Fđh = 12,82N.