Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

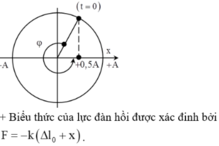
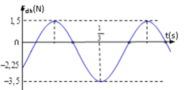
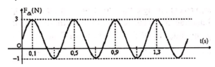
Từ hình vẽ với 2 vị trí cực đại và cực tiểu của lực đàn hồi ta có
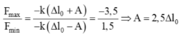
Tại t=0 và thời điểm lực đàn hồi cực đại ta có


Giải thích: Đáp án C
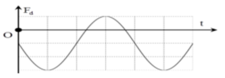
Từ đồ thị ta có hệ:
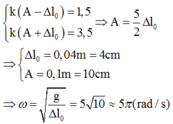
Biểu thức của lực đàn hồi có dạng: ![]()
Lúc t = 0, 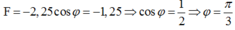

Giải thích: Đáp án C
Phương pháp:
Lưc̣ đàn hồi = (đô ̣cứng).(đô ̣biến dang̣)
Sử dung̣ đường tròn lượng giác
Cách giải:
Trục Ox thẳng đứng hướng xuống, gốc O trùng VTCB
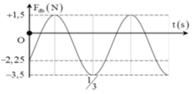
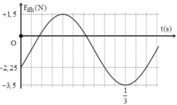
Từ đồ thị ta có:
Lực đàn hồi cực tiểu: Fmin = 0N
Lực đàn hồi giãn cực đại: ![]()
Lực đàn hồi nén cực đại: 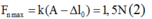
Từ (1) và (2) ![]()
Tại t = 0: ![]()
Ngay sau thời điểm t = 0 thì lực đàn hồi có độ lớn giảm => vật đang đi về phía VTCB
=> Tại t = 0: x = 5 và vật đi về phía vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có:
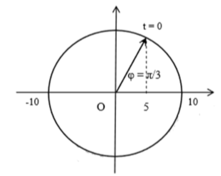
=> Pha ban đầu: φ=π/3
=> Phương trình dao động của vật: x = 10cos(5 πt + π/3)

Chọn A
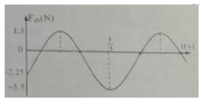
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
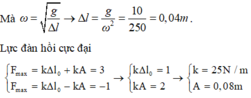
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.

Đáp án D
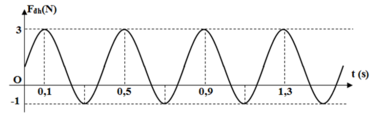
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
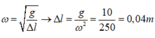
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 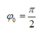 rad.
rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm

Đáp án D
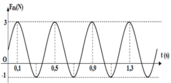
Độ giãn của con lắc ở vị trí cân bằng: T = 0,4 s = 2 π ∆ l 0 g ⇒ ∆ l 0 = T 2 g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
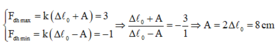
Độ cứng của lò xo: k = F d h m a x ∆ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
![]()
Tại thời điểm t = 0,1 s , lực đàn hồi có giá trị F = 3N nên:
F d h = 1 + 2 cos ( 5 π . 0 , 1 + μ ) = 3
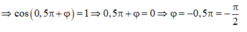
Phương trình dao động của vật: x = 8 cos ( 5 πt - π 2 ) ( c m )

Giải thích: Đáp án A
Phương pháp: Công thức tính lực đàn hồi ![]()
Cách giải :
Trong quá trình dao động của vật lò xo bị nén ![]()
Ta có 
Vậy thời gian lò xo bị nén trong một chu kì là 
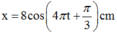
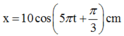
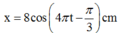
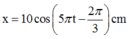



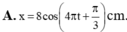
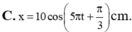
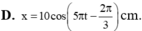
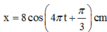
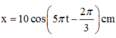
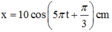
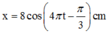
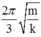
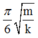
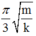
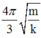
Giải thích: Đáp án B
Phương pháp: áp dụng công thức tính lực phục hồi của con lắc lò xo F =- kx và công thức tính lực đàn hồi