Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

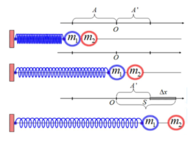
+ Giai đoạn 1: Cả hai vật cùng dao động với biên độ A, tần số góc ω = k m 1 + m 2 và tốc độ cực đại v 0 = ω A
+ Giai đoạn 2: Đến VTCB m2 tách ra khỏi m1 thì
*m1 dao động điều hòa với tần số góc ω ' = k m 1 và biên độ
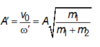
(vì tốc độ cực đại không đổi vẫn là v0!).
*m2 chuyển động thẳng đều với vận tốc v0 và khi m1 đến vị trí biên dượng (lần 1) thì m2 đi được quãng đường

Lúc này khoảng cách giữa hai vật:
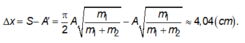

Đáp án B
Ban đầu hai vật cùng dao động với A = 8 ( c m ) và ω = k 2 m
Khi tới vị trí cân bằng chúng có v 0 = ω A thì chúng rời nhau; tiếp đó:
+ m 1 dao động với tốc độ cực đại vẫn là ω A nhưng với: ω ' = k m = ω 2 do đó A ' = A 2
+ m 2 chuyển động thẳng đều với vận tốc v 0 và sau thời gian t = T ' 4 = 1 4 . 2 π ω ' = π 2 ω 2 đi được s = v 0 t = A π 2 2
Vậy m 2 cách vị trí lúc đầu: s + A = 8 π 2 2 + 8 ≈ 16,9 ( c m )

Đáp án C
Phương pháp: Sử dụng phương pháp động lực học và phương pháp bảo toàn năng lượng.
Cách giải:
Hai vật chuyển động đến vị trí vận tốc cực đại, vị trí đó là :
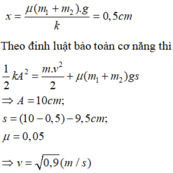
Khi hai vật tách nhau ra, vật 1 tiếp tục dao động, vật 2 chuyển động chậm dần rồi dừng lại.
Gia tốc chuyển động của vật 2 là:
![]()
Thời gian để vật 2 chuyển động đến khi dừng lại là:
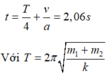

+ Sau một nửa chu kì thì biên độ của vật giảm 1 lượng là: ∆ A = 2 μ m g k
+ Sau một nửa chu kì thì biên độ của vật giảm 1 lượng là:
+ Độ giảm biên độ là:









Đáp án A
Ta có thể mô tả chuyển động của hệ hai vật thành các giai đoạn sau:
Giai đoạn 1: Hệ hai vật m 1 và m 2 dao động điều hòa quanh vị trí cân bằng (lò xo không biến dạng)
Tần số góc của dao động
Tốc độ của hệ tại vị trí cân bằng
Giai đoạn 2: Vật m 2 tách ra khỏi m 1 chuyển động thẳng đều với vận tốc v m a x , vật m 1 dao động điều hòa quanh vị trí cân bằng cũ.
Biên độ dao động của m 1 :
Khi lò xo có chiều dài lớn nhất → vật m 1 chuyển động ra biên, m 2 chuyển động với khoảng thời gian tương ứng
→ Khoảng cách giữa hai vật