

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A
Tại thời điểm cố định lò xo ta có E d = n E t E d + E t = E → E t = E n + 1 E d = n E n + 1
+ Vì thế năng đàn hồi của lò xo phân bố đều trên mỗi đơn vị chiều dài, do vậy thế năng của hệ dao động mới là E ' t = E t m = E m n + 1
+ Cơ năng của hệ dao động mới: E ' = E ' t + E ' d = E m n + 1 + n E n + 1 = 1 2 k ' A ' 2
Trong đó k′ = mk là độ cứng của phần lò xo tham gia vào dao động của vật lúc sau.
→ Biến đổi toán học ta thu được tỉ số A ' A = m n + 1 2 m n + 1

Đáp án A.
Sau khi giữ vật tại điểm chính giữa, vật sẽ dao động với lò xo có độ cứng k 1 = 2 k . Con lắc lò xo mới có chiều dài tự nhiên lo/2. Tại thời điểm giữ lò xo chiều dài con lắc này là x=A/2 tức là lò xo này đã giãn A/2.
Hay ly độ và vận tốc của vật lúc này là x = A/2 và v = 0 (do tại vị trí biên)
Suy ta, biên độ dao động sẽ là
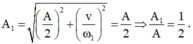 .
.

Tại thời điểm giữ lò xo thì: \(W_{d}=W_{t}=\dfrac{W}{2}\)
Cố định 1 điểm chính giữa lò xo thì thế năng giảm đi 1 nửa
\(\Rightarrow W_{t'}=\dfrac{W_t}{2}=\dfrac{W}{4};W_{đ}=\dfrac{W}{2}\Rightarrow W'=\dfrac{3W}{4}\)
Có: \(k'=2k\Rightarrow \dfrac{3}{4}.kA^{2}=k'A'^{2}\)
\(\Rightarrow \dfrac{A}{A'}=\dfrac{4}{\sqrt{6}}\)

Hướng dẫn:
+ Khi vật đi qua vị trí li độ 4 cm, ta giữ điểm chính giữa, khi đó cơ hệ mới có lò xo giãn 2 cm
→ Tốc độ của vật khi vừa mới giữ điểm chính giữa v 0 = ω A 2 − x 2 = 2 π .5 5 2 − 4 2 = 30 π c m / s
+ Biên độ dao động mới của con lắc
A ' = x 0 2 + v 0 ω ' 2 = 2 2 + 30 π 2 π .5 2 2 = 2 , 92 c m
Đáp án A