Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

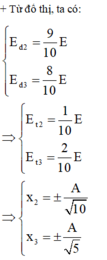
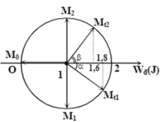
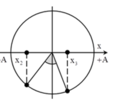
→ Biểu diễn các vị trí tương ứng trên hình tròn, ta thu được:
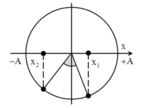
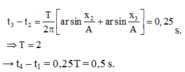
Đáp án C

Đáp án C
Con lắc dao động điều hòa theo phương thẳng đứng
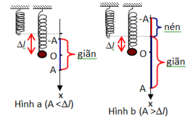
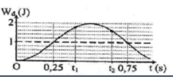
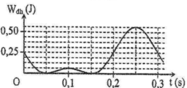
Từ đồ thị => gốc thế năng đàn hồi ở vị trí lò xo có độ dài tự nhiên và thuộc trường hợp A>Δl
Từ đồ thị ta có mỗi dòng ngang có mức thế năng: 0,25 /4 = 0,0625J.
Ta có, thế năng đàn hồi của lò xo: W t = 1 2 k x 2 (x là độ biến dạng của lò xo so với vị trí lò xo có độ dài tự nhiên). Từ đồ thị ta thấy:
+ Tại vị trí lò xo không biến dạng: Wt = 0
+ Tại vị trí vật lên cao nhất: x= A-Δl -> thế năng đàn hồi:
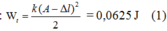
+ Tại vị trí vật xuống thấp nhất:x= A+Δl -> thế năng đàn hồi cực đại :
![]()
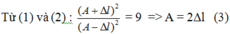
+ Chu kì dao động của con lắc:T= 0,3s
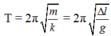
![]()
Suy ra A =2Dl0 = 4,5cm. Từ k ( A - ∆ l ) 2 2 = 0 , 0625
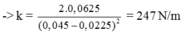
Từ T = 2 π m k
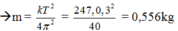

Chọn A
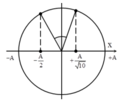
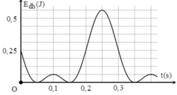
Ta xét các tỉ số: x 1 A 1 2 = E − E d 1 E = 4 − 3 4 = 1 4 x 2 A 1 2 = E − E d 2 E = 4 − 3 , 6 4 = 1 10 → x 1 = ± A 2 x 2 = ± A 10
Biểu diễn dao động của vật tương ứng trên đường tròn, ta có t 2 − t 1 m a x = T 360 a r cos 1 2 + T 360 a r cos 1 10 ≈ 0 , 404
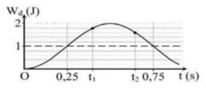
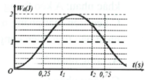
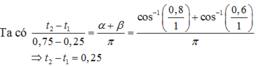


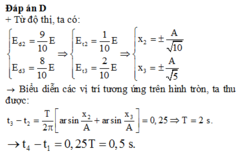

Giải thích: Đáp án B
Phương pháp: Công thức tính năng lượng của con lắc lò xo
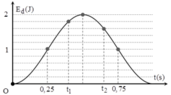
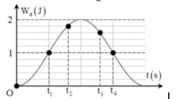
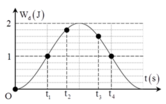
Từ đồ thị ta có Wdmax = W = 2J và lúc t = 0 thì Wd = 0 Vật ở vị trí biên
Từ VTLG suy ra thời gian t2 – t1 tương ứng với góc quét được tô đậm trên hình: