Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ü Đáp án C
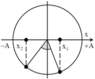
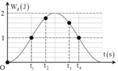
+ Từ đồ thị, ta có:
E d 2 = 9 10 E E d 3 = 8 10 E ⇒ E t 2 = 1 10 E E t 3 = 2 10 E ⇒ x 2 = ± A 10 x 3 = ± A 5
→ Biểu diễn các vị trí tương ứng trên hình tròn, ta thu được:
t 3 - t 2 = T 2 π a r sin x 2 A + a r sin x 3 A = 0 , 25 ⇒ T = 2 s
→ t4 – t1 = 0,25T = 0,5 s
Đáp án C
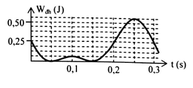
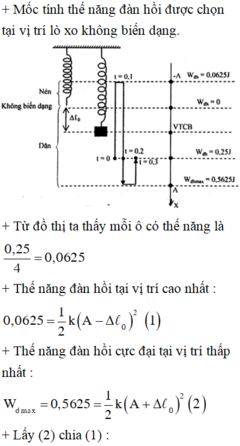
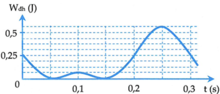
Mốc tính thế năng đàn hồi được chọn tại vị trí lò xo không biến dạng.
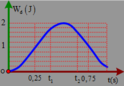
Từ đồ thị ta thấy mỗi ô có thế năng là 0 , 25 4 = 0 , 0625
Thế năng đàn hồi tại vị trí cao nhất: 0 , 0625 = 1 2 k A − Δ l 0 2 ( 1 )
Thế năng đàn hồi cực đại tại vị trí thấp nhất: W d max = 0 , 5625 = 1 2 k A + Δ l 0 2 ( 2 )
Lấy (2) chia (1): 9 = A + Δ l 0 2 A − Δ l 0 2 ⇒ 3 = A + Δ l 0 A − Δ l 0 ⇒ A = 2 Δ l 0 ( 3 )
Từ đồ thị ta thấy chu kì dao động của con lắc là: T = 0 , 3 s
Mặt khác con lắc lò xo treo có chu kì:
T = 2 π m k = 2 π Δ l 0 g ⇒ Δ l 0 = T 2 g 4 π 2 = 0 , 3 2 π 2 4 π 2 = 0 , 0225 m = 2 , 25 c m
⇒ A = 2 Δ l 0 = 4 , 5 c m Thế vào (1): k = 2.0 , 0625 A − Δ l 0 2 = 2.0 , 0625 0 , 045 − 0 , 0225 2 = 247 N / m
⇒ m = T 2 k 4 π 2 = 0 , 3 2 .247 4 π 2 = 0 , 56 k g
Chú ý: Gốc thế năng đàn hồi được chọn tại vị trí lò xo không dãn.
Đáp án C
Trên đồ thị ta có:
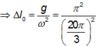
độ biến dạng của lò xo ở VTCB
Chọn chiều dương hướng xuống, gốc tọa độ O tại VTCB, gốc thế năng tại vị trí lò xo không biến dạng. Biểu thức thế năng đàn hồi: 
Từ đó:
- Tại vị trí 
thì
W
t
=
0
- Tại vị trí 
thì 
Tại vị trí 
thì 
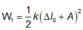
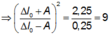
( suy từ các biểu thức thế năng)
Và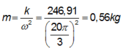 
Đáp án A
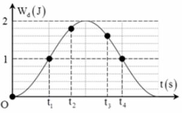
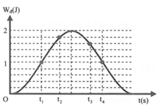
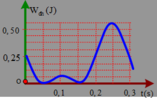
Vì thời điểm t = 0 , 1 s ở giữa hai thời điểm thế năng đàn hồi bằng 0 nên lúc này vật đang ở vị trí biên âm.
Lúc này: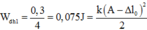 
Tại thời điểm t 2 = 0 , 2 s thì lò xo ở biên dương
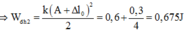
Từ đó suy ra:
Dễ thấy:
Nên 
STUDY TIP
Bài toán trên nếu chúng ta nhầm lẫn giữa thế năng đàn hồi và thế năng thì chúng ta sẽ nhận được kết quả sai. Thế năng của hệ thì gồm cả thế năng đàn hồi và thế năng hấp dẫn.
Chọn đáp án B