Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Chu kỳ của con lắc khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc a là:
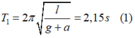
Chu kỳ của con lắc khi thang máy chuyển động thẳng đứng đi lên chậm dần đều với gia tốc a là:
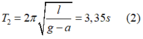
Chia (1) cho (2) ta được: a = 0,42g
Thay giá trị của a vào (1) ta được:
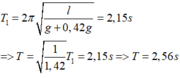
Với T là chu kỳ của con lắc khi thang máy không chuyển động

Chọn D.
K h i t h a n g đ ứ n g y ê n : T = 2 π l g K h i t h a n g c h u y ể n đ ộ n g n h a n h d ầ n đ ề u : T 1 = 2 π l g + a K h i t h a n g c h u y ể n đ ộ n g c h ậ m d ầ n đ ề u : T 2 = 2 π l g - a
Ta rút ra hệ thức:
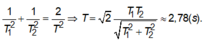

Chọn D
*Khi thang máy đi lên nhanh dần đều với đi xuống chậm dần đều với độ lớn gia tốc a ta có gia tốc biểu kiến lần lượt là:
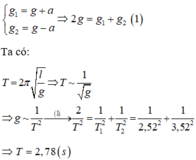

Chọn đáp án D
* Khi thang máy đi lên nhanh dẩn đều với đi xuống chậm dần đều với độ lớn gia tốc a ta có gia tốc biểu kiến lần lượt là: g 1 = g + a g 2 = g − a ⇒ 2 g = g 1 + g 2 1
Ta có: T = 2 π l g ⇒ T ~ 1 g ⇒ g ~ 1 T 2 → ( 1 ) 2 T 2 = 1 T 1 2 + 1 T 2 2 = 1 2 , 52 2 + 1 3 , 52 2
⇒ Τ = 2 , 78 s

Đáp án C
+ Chu kì của con lắc khi thang máy đứng yên và khi thang máy chuyển động đi lên chậm dần đều:
T = 2 π l g T ' = 2 π l g - 0 , 5 g → T ' = T 2

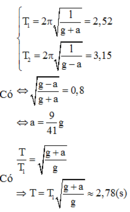
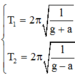
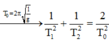

Đáp án D
Ta có T 1 = 2 π 1 g + a 1 , T 2 = 2 π 1 g − a 2 , T = 2 π 1 g 3
Từ (1); (2) và (3) ta được 2 T 2 = 1 T 1 2 + 1 T 2 2 ⇒ T = 3 , 4 s