Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

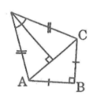
a. Nối AC và kẻ DH ⊥ AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
A C 2 = A B 2 + B C 2 = 12 2 + 12 2 = 144 + 144 = 288
Suy ra: AC = 12 2 (cm)
Ta có: ∆ ACD cân tại D
DH ⊥ AC
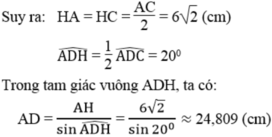

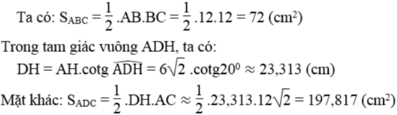
Vậy S d i ề u = S A B C + S A D C = 72 + 197 , 817 = 269 , 817 c m 2

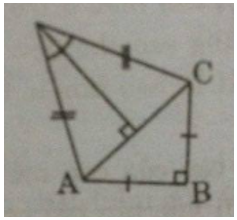
a) Nối AC và kẻ DH⊥ACDH⊥AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2=AB2+BC2=122+122=144+144=288AC2=AB2+BC2=122+122=144+144=288
Suy ra: AC=12√2(cm)AC=122(cm)
Ta có: tam giác ACD cân tại D
DH⊥ACDH⊥AC
Suy ra: HA=HC=AC2=6√2(cm)HA=HC=AC2=62(cm)
ˆADH=12ˆADC=20∘ADH^=12ADC^=20∘
Trong tam giác vuông ADH, ta có:
AD=AHsinˆADH=6√2sin20∘≈24,809(cm)AD=AHsinADH^=62sin20∘≈24,809(cm)
b) Ta có:
SABC=12.AB.BC=12.12.12=72SABC=12.AB.BC=12.12.12=72 (cm2)
Trong tam giác vuông ADH, ta có:
DH=AH.cotgˆADH=6√2.cotg20∘≈23,313(cm)DH=AH.cotgADH^=62.cotg20∘≈23,313(cm)
Mặt khác:
SADC=12.DH.AC≈12.23,313.12√2=197,817SADC=12.DH.AC≈12.23,313.122=197,817 (cm2)
Vậy Sdiều =SABC+SADC=72+197,817=269,817=SABC+SADC=72+197,817=269,817 (cm2)
a, nối AC rồi kẻ
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC:
Suy ra:
ta có:tam giác ABC cân tại D
Suy ra:
Trong tam giác vuông ADH, ta có
b, Ta có:
(cm2)
Trong tam giác vuông ADH, ta có:
Mặt khác
(cm2)
Vậy S (cm2)

Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~


a) Có nhiều cách tính diện tích AICJ. Chẳng hạn:
C1: Do I, J là trung điểm AB, AD nên \(AI=AJ=\frac{1}{2}\)
Ta thấy ngay \(\Delta AJC=\Delta AIC\left(c-g-c\right)\Rightarrow S_{AJC}=S_{AIC}\)
Vậy thì \(S_{AICJ}=2S_{AIC}=2.\frac{1}{2}AI.CB=\frac{1}{2}\left(đvdt\right)\)
C2:
Do I, J là trung điểm AB, AD nên \(AI=AJ=\frac{1}{2}\)
Ta thấy ngay \(\Delta DJC=\Delta BIC\) (Hai cạnh góc vuông) \(\Rightarrow S_{DJC}=S_{BIC}\)
Vậy thì \(S_{AICJ}=S_{ABCD}-2S_{BIC}=1-\frac{1}{2}=\frac{1}{2}\left(đvdt\right)\)
b)
C1: Xét tam giác DJC có \(tan\widehat{DCJ}=\frac{JD}{DC}=\frac{1}{2}\Rightarrow\widehat{DCJ}\approx26^o34'\)
\(\Rightarrow\widehat{JCA}=45^o-\widehat{DCJ}\Rightarrow\widehat{ICJ}=90^o-2\widehat{DCJ}\)
Dúng máy tính ta tìm được \(\sin\widehat{ICJ}=\frac{3}{5}\)
C2: Theo Pytago thì \(JC=\sqrt{1+\frac{1}{4}}=\frac{\sqrt{5}}{2}\)
Ta thấy ngay \(S_{AIJ}=\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}\)
\(\Rightarrow S_{IJC}=\frac{1}{2}-\frac{1}{8}=\frac{3}{8}\)
Kẻ IH vuông góc JC.
Ta tìm được \(IH=2S_{IJC}:JC=2.\frac{3}{8}:\frac{\sqrt{5}}{2}=\frac{3\sqrt{5}}{10}\)
\(\Rightarrow\sin\widehat{ICJ}=\frac{IH}{IC}=\frac{3}{5}.\)
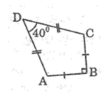
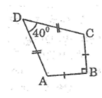
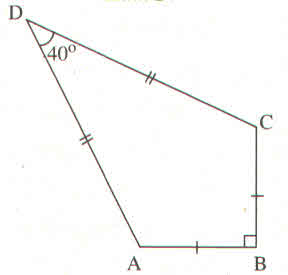
Xét ΔABC có:
.AB=BC=12cm
.\(\widehat{ABC}=90^o\)
➜ΔABC vuông cân tại B
➜AC=AB\(\sqrt{2}\) =12\(\sqrt{2}\) (cm)
Gọi H là trung điểm AC
➜AH=6\(\sqrt{2}\) (cm)
Xét ΔADC có: AD=DC
➜ΔADC cân tại D
mà: H là trung điểm AC
➜DH là đường cao, cũng là đường phân giác của ΔADC
➜\(\widehat{ADH}=20^O\)
\(\sin\widehat{ADH}=sin20^o=\dfrac{AH}{AD}\)
➜\(AD=\dfrac{AH}{\sin20^o}=\dfrac{6\sqrt{2}}{\sin20^o}=24,8\left(cm\right)\)
b, SABCD= SABC+SADC
SABCD = \(\dfrac{1}{2}.AB.BC+\dfrac{1}{2}.AC.DH\)
\(\cos\widehat{ADH}=\dfrac{DH}{AD}=\cos20^O\)
➜\(DH=\cos20^O.AD=\cos20^O.24,8=23,3\left(cm\right)\)
SABCD= \(\dfrac{1}{2}.12.12+\dfrac{1}{2}.12\sqrt{2}.23,3=269,7\left(cm^2\right)\)