Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Giả sử cái cổng hình bán nguyệt có dạng như hình vẽ
Cái cổng là nửa hình tròn có bán kính \(R=3,4m\)
Phương trình mô phỏng cái cổng là phương trình đường tròn tâm \(O\left(0;0\right)\)bán kính \(R=3,4m\) có dạng: \(x^2+y^2=11,56\)
b. Chiếc xe tải rộng \(2,4m\); cao \(2,5m\) ta có toạ độ điểm xa nhất của xe tải so với tâm của cổng là điểm \(M\left(2,4;2,5\right)\)
Ta có độ dài đoạn: \(OM=\left|\overrightarrow{OM}\right|\) mà \(\overrightarrow{OM}\left(2,4;2,5\right)\)
Vậy: \(\left|\overrightarrow{OM}\right|=\sqrt{2,4^2+2,5^2}\approx3,5\) suy ra độ dài đoạn thẳng \(OM=3,5m>R\)
Vì điểm xa nhất của xe tải lớn hơn bán kính đường tròn khi đi đúng làn đường xe tải không qua được cổng.
Lời giải
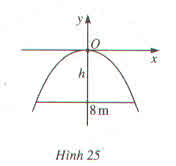
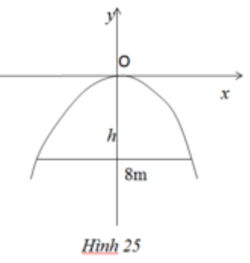
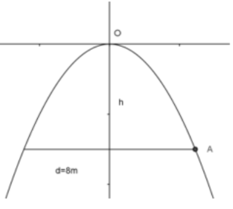
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m