Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Ta có V = a b c S = 2 a b + b c + c a . Theo đề ta có:
a b c = 2 a b + b c + c a ; 1 ≤ a ≤ b ≤ c ⇔ 1 = 2. a b + b c + c a a b c ⇔ 2 a + 2 b + 2 c = 1
Ta có 1 = 2 a + 2 b + 2 c ≤ 2 a + 2 a + 2 a = 6 a ⇒ a ≤ 6 . Kết hợp với 2 a + 2 b + 2 c = 1 ta có:
a = 3 ⇒ 1 b + 1 c = 1 6 ⇒ 6 < b ≤ 12
⇒ a ; b ; c e { 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 }
Với a = 4 ⇒ 1 b + 1 c = 1 4 ⇒ 4 < b ≤ 8 ⇒ a ; b ; c ∈ 4 ; 5 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8
với a = 5 ⇒ 1 b + 1 c = 3 10 < 1 3 ⇒ b < 6 ⇒ a ; b ; c ∈ 5 ; 5 ; 10
với a = 6 ⇒ 1 b + 1 c = 1 3 ⇒ b ≤ 6 ⇒ a ; b ; c ∈ 6 ; 6 ; 6
⇒ a ; b ; c ∈ 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 4 ; 6 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8 , 5 ; 5 ; 10 , 6 ; 6 ; 6
Vậy ta chọn B.

Đặt ![]() khi đó yêu cầu bài toán trở thành phương trình
khi đó yêu cầu bài toán trở thành phương trình
![]() có nghiệm
t
∈
(
0
;
1
]
Có
có nghiệm
t
∈
(
0
;
1
]
Có
![]()
Do đó
![]()
![]()
![]()
Vậy ![]()
Tổng các phần tử của tập S bằng -10.
Chọn đáp án D.

Đáp án C.
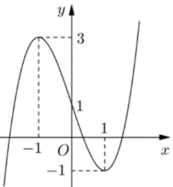
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
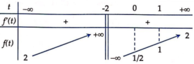
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng

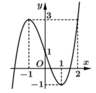
Đặt t = sinx do ![]()
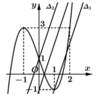
● Gọi ∆ 1 là đường thẳng qua điểm (1;-1) và song song với đường thẳng y = 3x nên có phương trình y = 3x - 4
● Gọi ∆ 2 là đường thẳng qua điểm (0;1) và song song với đường thẳng y = 3x nên có phương trình y = 3x+1
Do đó phương trình
f
sin
x
=
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
khi và chỉ khi phương trình f(t) = 3t + m có nghiệm thuộc nửa khoảng ![]() Chọn A.
Chọn A.
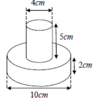
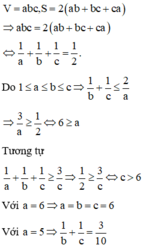
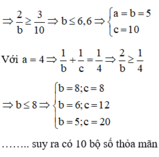



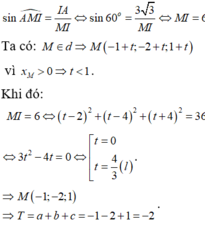
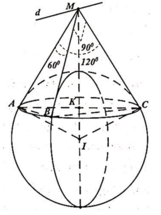
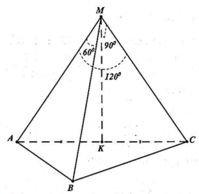

Đáp án C
Diện tích bề mặt bằng tổng diện tích toàn phần của hình trụ lớn và diện tích xung quanh của hình trụ nhỏ. Do đó:
S = 2 π .5 2 + π 5.2 + 2 π .2.5 = 90 π c m 2
Thể tích của chi tiết máy bằng tổng thể tích của 2 hình trụ. Do đó: V = π .5 2 .2 + π 2 2 .5 = 70 π c m 3