Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Ta có: T 2 = t 2 − t 1 = 0 , 75 ( s )
⇒ T = 1 , 5 ( s ) ; v ¯ t b = 2 A T / 2 = 16 ( m / s ) ⇒ A = 6 ( c m )
Lại có: t 1 = 2 T + T 6 ⇒ Tại t1 thì vật sẽ cùng vị trí với vật tại thời điểm t = T 6
Tại t 1 vật có li độ x 0 = A
Vậy tại thời điểm ban đầu t 0 vật sẽ có li độ là x = A 2 = 3 ( c m )

Biểu diễn vị trí đó trên giản đồ véc tơ ta có:
Như vậy, giữa 2 lần liên tiếp chất điểm cách VTCB 3cm ứng với véc tơ quay từ M-N-P-Q.
\(\Rightarrow A.\cos 45^0=3\)
\(\Rightarrow A = 3.\sqrt 2\) (cm)

Chọn C
+ ω = 2π : T = 20 rad/s.
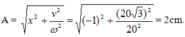
+ t = 0: x = 2cosφ = -1 => 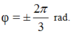
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.

Đáp án B
Giả sử x = Acos ( ωt + φ )
Thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là nửa chu kỳ nên
![]()
Quãng đường đi được trong 2s (2 chu kì) là: S=2.4A=32 =>A=4cm
Tại thời điểm t=1,5s vật qua vị trí có li độ 2 3 cm theo chiều dương
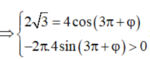
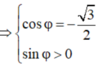
Suy ra, có thể lấy φ = - 7 π 6

+ Khi \(W_đ=3W_t\Rightarrow W=4W_t\Rightarrow x=\pm\frac{A}{2}\)
+ Khi \(W_đ=\frac{1}{3}W_t\Rightarrow W=\frac{4}{3}W_t\Rightarrow x=\pm\frac{\sqrt{3}}{2}A\)
Ta có véc tơ quay như sau:
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(t=\frac{30}{360}T=\frac{1}{12}.2=\frac{1}{6}s\)
\(S=\left(\frac{\sqrt{3}}{2}-\frac{1}{2}\right).10=\left(\sqrt{3}-1\right).5\)
Tốc độ trung bình: \(v=\frac{S}{t}=\left(\sqrt{3}-1\right).30=21,96\)(cm/s)



Chọn D