Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.

Vì có n khoảng thời gian đi 3s và (n-1) khoảng thời gian nghỉ 1s nên tổng thời gian cả đi và nghỉ: t = 3n + (n – 1) = 4n – 1(s)
Quãng đường đi:


Chọn D.
Vì có n khoảng thời gian đi 3s và (n – 1) khoảng thời gian nghỉ 1s nên tổng thời gian cả đi và nghỉ: t = 3n + (n – 1) = 4n – 1(s)
Quãng đường đi:
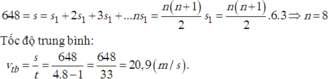

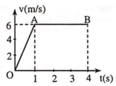
a) Gia tốc trên đoạn OA: a 1 = Δ v Δ t = 6 1 = 6 m/s2.
Trên đoạn AB chất điểm chuyển động thẳng đều nên gia tốc a 2 = 0 .
b) Quãng đường chất điểm đi trong 1s đầu tiên: s 1 = 1 2 a 1 t 1 2 = 1 2 .6.1 2 = 3 m.
Quãng đường chất điểm đi trong 2s kế tiếp: s 2 = v t 2 = 6.2 = 12 m.
Quãng đường chất điểm đi trong 3s đầu tiên: s 2 = v t 2 = 6.2 = 12 m.
c) Thời điểm mà chất điểm có vận tốc 2,4m/s: t = v a = 2 , 4 6 = 0 , 4 s.

a, a=v/t=2m/s
b, \(S=\dfrac{1}{2}at^2=100\left(m\right)\)
đi được trong 9s \(S_9=\dfrac{1}{2}a9^2=81\left(m\right)\)
quãng đường đi trong giây 10 \(S_{10}=S-S_9=100-81=19\left(m\right)\)
c, \(S_6=\dfrac{1}{2}a6^2=36\left(m\right)\)
vận tốc sau khi đi 1/4 S6 \(v'=a.t=2.\sqrt{\dfrac{\dfrac{2.1}{4}.36}{2}}=6\left(m/s\right)\)
27 m còn lại là 3/4S6
ta có \(27=6.t+\dfrac{1}{2}2.t^2\Rightarrow t=3\left(s\right)\)

Đáp án B.
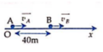
Nhận xét: Khoảng cách giữa hai chất điểm nhỏ nhất khi:
vB = vA ⇔ 0+2t=10
⇒ t = 5s
Lúc này chất điểm chuyển động từ A đã đi được s1=5.10=50m
Và chất điểm chuyển động từ B đã đi được
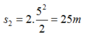
Khoảng cách nhỏ nhất bằng s2 - s1+40 = 25-50+40=15

a) Từ công thức v 2 − v 0 2 = 2 a s ⇒ gia tốc: a = v 2 − v 0 2 2 s
Thay số ta được: a = 8 2 − 4 2 2.8 = 3 m/s2.
b) Phương trình chuyển động có dạng: x = v 0 t + 1 2 a t 2 .
Thay số ta được: x = 4 t + 1 , 5 t 2 (m).
c) Ta có: v = v 0 + a t ⇒ t = v − v 0 a = 13 − 4 3 = 3 s.
Tọa độ của chất điểm lúc đó: x = 4.3 + 1 , 5.3 2 = 25 , 5 m.
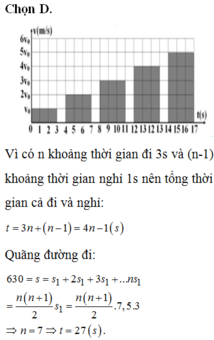
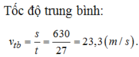
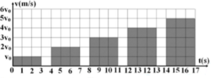

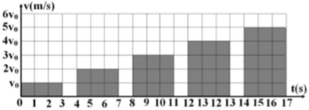
Tổng quãng đường chất điểm chuyển động là:
\(S=v_0t+2v_0t+...+nv_0t\)
\(S=\left(1+2+...+n\right)v_0t=\frac{n\left(n+1\right)}{2}v_0t\)
Tại sao lại có \(\left(1+2+...+n\right)v_0t=\frac{n\left(n+1\right)}{2}v_0t?\)
Công thức tính tổng dãy số học tiểu học:
Số số hạng: \(\frac{\left(n-1\right)}{1}+1=n\left(so-hang\right)\)
Tổng: \(\frac{\left(n+1\right).n}{2}\)
Làm tiếp đoạn kia:
\(\frac{n\left(n+1\right)}{2}v_0t=315\Leftrightarrow n\left(n+1\right)=\frac{315.2}{5.3}=42\)
\(\Leftrightarrow n^2+n-42=0\Leftrightarrow n=6\)
Vậy chất điểm chuyển động 6 lần và nghỉ 5 lần ( (ko tính lần nghỉ sau khi đến B)
\(\Rightarrow v_{tb}=\frac{S}{t}=\frac{315}{3.6+5}\approx13,7\left(m/s\right)\)