Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B

Chọn B.
Khoảng cách giữa M và N là:

Khoảng cách lớn nhất khi MN có phương nằm ngang
⇒ 6 2 + 8 2 = 10 2 ⇒ OM luôn vuông góc với ON. Ở thời điểm mà M có động năng bằng thế năng tại x M = A 2 2
tức OM hợp với Ox góc π / 4 => ON hợp với Ox góc π / 4 hay
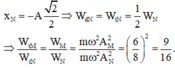

Chọn đáp án A
Thời gian ngắn nhất đi từ x = A đến x = A 2 là T/6

Chọn đáp án A
Thời gian ngắn nhất đi từ x = A đến x = A 2 là T 6
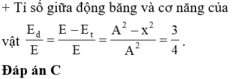
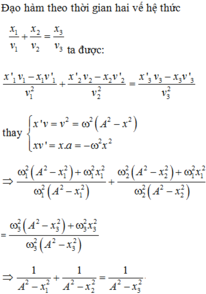
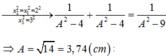

Đáp án A
Đây là vật dao động điều hòa với vị trí cân bằng tại B → biên dương có tọa độ A +B, biên âm có tọa độ B – A