Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bt1:
\(s=3,6km=360m\\ t=40p=2400s\\ \Rightarrow v=\dfrac{s}{t}=\dfrac{360}{2400}=0,15\left(\dfrac{m}{s}\right)\\ Đổi:0,15\dfrac{m}{s}=0,54\dfrac{km}{h}\)
Bt2:
\(v=20\dfrac{km}{h}\\ t=30p=0,5h\\ \Rightarrow s=v.t=20.0,5=10\left(km\right)\)
Bt3:
\(s=1,5km=1500m\\ v=10\dfrac{m}{s}\\ \Rightarrow t=\dfrac{s}{v}=\dfrac{1500}{10}=150\left(s\right)\)

ta có:
thời gian người đó đi trong nửa quãng đường đầu là:
t1\(=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{40}\left(1\right)\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S}{t_1+t_2+t_3}=\frac{S}{t_1+t'}\left(3\right)\)
ta lại có:
S2+S3=S/2
\(\Leftrightarrow v_2t_2+v_3t_3=\frac{S}{2}\)
\(\Leftrightarrow\frac{15t'}{2}+\frac{25t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow40t'=S\Rightarrow t'=\frac{S}{40}\left(2\right)\)
thế (1) và (2) vào phương trình trên ta có:
\(v_{tb}=\frac{S}{\frac{S}{40}+\frac{S}{40}}=\frac{S}{S\left(\frac{2}{40}\right)}=\frac{1}{\frac{2}{40}}=20\)
quãng đường người đó đã đi là:
S=vtb.t=60km
vậy AB dài 60km

Em thứ nhất chạy nhanh hơn em thứ hai nên trong thời gian t0 = 1s em thứ nhất chạy hơn em thứ hai một đoạn đường là:
s = s1 – s2 = v1.t0 – v2.t0 = 4,8.1 – 4.1 = 0,8m.
Sau khoảng thời gian t (s), quãng đường em thứ nhất chạy hơn em thứ hai là:
S = 0,8.t
Em thứ nhất sẽ gặp em thứ hai lần đầu tiên sau thời gian t (s) khi mà quảng đường em thứ nhất chạy hơn em thứ hai trong khoảng thời gian đó bằng đúng chu vi một vòng chạy.
Khi đó ta có: S = 0,8.t = Cchu vi = 400 m
Suy ra (v1 – v2).t = 400.
Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy là:
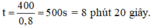

a.Gọi s là chiều dài quãng đường AB
tx,tn lần lượt là thời gian xuôi dòng và ngược dòng của thuyền
Đổi 2h30'=2,5h
Quãng đường đi xuôi dòng là:
s=tx*vx=18*tx(1)
Quãng đường ngược dòng là:
s=tn*vn=12*tn(2)
Từ (1);(2) => 18*tx = 12*tn => tx = 2/3tn
Lại có: tx+tn=2,5
=>tn=1,5h
Khoảng cách AB là 1,5*12=18(km)
(dài quá không giải nữa đâu. Bạn phải hỏi từng câu 1 đi)
Theo cách mình nghĩ thfi thời gian ngắn nhất chạy từ A-->E-->C.
Thời gian người đó đi hết khu cỏ là: \(t_{cỏ}=\dfrac{AE}{v}=\dfrac{AD}{3v}\)
\(EC=\sqrt{ED^2+DC^2}\)
\(\Leftrightarrow EC=\sqrt{\dfrac{4}{9}AD+DC^2}\)
Thời gian người đó đi từ A-C là: \(t_{đất}=\dfrac{EC}{v'}=\dfrac{\sqrt{\dfrac{4}{9}AD+DC^2}}{1,5v}\)
\(t_{Min}=t_{cỏ}+t_{đất}=\dfrac{AD}{3v}+\dfrac{\sqrt{\dfrac{4}{9}AD+DC^2}}{1,5v}\)
Hung nguyen h giải seo