Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của ca nô lúc dòng nước yên lặng là x (km/h); (x > 2)
Vì vận tốc nước là 2 km/h nên vận tốc xuôi dòng và ngược dòng lần lượt là x + 2 và x – 2 (km/h)
Thời gian để ca nô đi hết 42 km xuôi dòng là 42/(x+2) (h)
Thời gian để ca nô đi hết 20 km ngược dòng là 20/(x-2) (h)
Tổng thời gian là 5h do đó
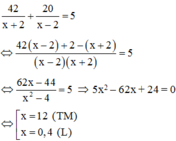
Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h
Đáp án: B

Gọi x (km/h) là vận tốc thực của canô (x>2)
Khi đi ngược dòng thì vận tốc của canô là: x-2 (km/h)
Đổi: 4 giờ 30 phút = 4,5 giờ
Theo đề bài, ta có phương trình:
\(\frac{40}{x-2}+\frac{40}{x+2}=4,5\)
\(\Leftrightarrow40\left(x+2\right)+40\left(x-2\right)=4,5\left(x^2-4\right)\)
\(\Leftrightarrow80x=4,5x^2-18\)
\(\Leftrightarrow\left(x-18\right)\left(4,5x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=18\left(TM\right)\\x=-\frac{2}{9}\left(KTM\right)\end{cases}}\)
Vậy vận tốc thực của canô là: 18 km/h

Quãng đường ca nô đi từ bến A đến B rồi lại lập tức quay trở ngược lại bến A là :
45 x 2 = 90 (km)
Đổi 6h15` = 6,25h
Vận tốc của ca nô là :
90 : 6,25 = 14,4 (km/h)
Mình nghĩ bạn cho thừa dữ kiện là V dòng nước
Quãng đường ca nô đi từ bến A đến B rồi lại quay trở ngược lại bến A là :
45 x 2 = 90 (km)
Đổi 6 giờ15 phút = 6,25 giờ
Vận tốc của ca nô khi nước lặng là :
90 : 6,25 = 14,4 (km/ giờ)
Đáp số : 14,4 km / giờ

6h15'= 25/4 h
gọi vận tốc của cano khi nước yên lặng là x (km) (x>3)
vận tốc khi cano xuôi dòng là: x+3 (km/h)
..........................ngược..........: x-3(km/h)
thời gian cano xuôi dòng 45km là: \(\frac{45}{x+3}\)(h)
.....................ngược......................: \(\frac{45}{x-3}\)(h)
do cả đi cả về hết 25/4 h nên ta có phương trình:
\(\frac{45}{x+3}+\frac{45}{x-3}=\frac{25}{4}\)
đến đay bạn tự giải phương trình sau đó kết luận nhé !!
#chúc bạn học tốt

Gọi vận tốc thực của ca nô là x ( km/h ; x > 4 )
Vận tốc khi ca nô xuôi dòng = x + 4 (km/h)
Vận tốc khi ca nô ngược dòng = x - 4 (km/h)
Thời gian ca nô xuôi dòng = 136/x+4 (giờ)
Thời gian ca nô ngược dòng = 91/x-4 (giờ)
Tổng thời gian xuôi dòng và ngược dòng là 7h30' = 15/2h
=> Ta có phương trình : \(\frac{136}{x+4}+\frac{91}{x-4}=\frac{15}{2}\)
<=> \(\frac{136\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}+\frac{91\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\frac{15}{2}\)
=> 15( x2 - 16 ) = 2( 227x - 180 )
<=> 15x2 - 454x + 120 = 0
Δ' = b'2 - ac = (-227)2 - 15.120 = 49 729
Δ' > 0, áp dụng công thức nghiệm thu được x1 = 30 (tm) ; x2 = 4/15 (ktm)
Vậy vận tốc thực của ca nô là 30km/h

Gọi vận tốc cano khi mặt nước yên lặng là x (km/h) (x>3)
Ta có : Vận tốc cano khi xuôi dòng là : x + 3 (km/h)
Vận tốc cano khi ngược dòng là : x - 3 (km/h)
Phương trình : \(\frac{15}{x+3}+\frac{20}{60}+\frac{15}{x-3}=3\)
\(\Leftrightarrow\frac{1}{x+3}+\frac{1}{x-3}=\frac{8}{45}\)
Giải phương trình trên ta được x = 12 (vì x>0)
Vậy : Vận tốc cano khi nước yên lặng là 12 km/h

Gọi vận tốc thực của ca nô là x (x > 0, km/h)
Đổi 15 phút = 15 60 = 1 4 h
*) Xuôi dòng:
Vận tốc của ca nô là x + 4 (km/h) → Thời gian xuôi dòng của ca nô là 80/(x+4) (h)
*) Ngược dòng
Vận tốc ngược dòng của ca nô là x – 4 (km/h) → Thời gian ngược dòng của ca nô là 72/(x-4) (h)
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút nên ta có phương trình:
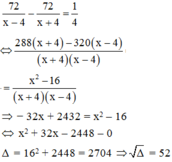
Phương trình có hai nghiệm
x = −16 + 52 = 36 (tmdk)
x = −16 – 52 = −68 (loại)
Vậy vận tốc thực của ca nô là 36 km/h
Đáp án: A