Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

15 phút = (1/4)giờ
Gọi vận tốc của ca nô khi nước đứng yên là x (km/h). Điều kiện x > 2
Vận tốc ca nô khi xuôi dòng là x + 2 (km/h)
Vận tốc ca nô khi ngược dòng là x – 2 (km/h)
Thời gian ca nô khi xuôi dòng là:
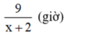
Thời gian ca nô khi ngược dòng là:
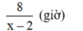
Ta có phương trình:
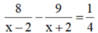
Quy đồng mẫu hai vế:
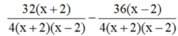
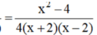
Suy ra:
32x + 64 - 36x + 72 = x2 - 4
⇔ -4x + 136 = x2 - 4
⇔ x2 + 4x - 140 = 0
⇔ (x2 + 4x + 4) - 144 = 0
⇔ (x + 2)2 - 122 = 0
⇔ (x + 14)(x - 10) = 0
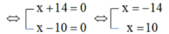
Giá trị x = -14 không thỏa mãn điều kiện
Giá trị x = 10 thỏa mãn điều kiện
Vậy vận tốc của ca nô khi nước yên lặng là 10km/h

Gọi vận tốc thực của cano là x(km/h) (x>1)
Vận tốc xuôi dòng: x+1 (km/h)
Vận tốc ngược dòng x - 1(km/h)
Thời gian xuôi dòng: \(\dfrac{60}{x+1}\)(h)
Thời gian ngược dòng : \(\dfrac{60}{x-1}\left(h\right)\)
Theo bài ta có :
\(\dfrac{60}{x-1}-\dfrac{60}{x+1}=1\)
=> \(\dfrac{60\left(x+1\right)}{x^2-1}-\dfrac{60\left(x-1\right)}{x^2-1}=\dfrac{x^2-1}{x^2-1}\)
=> 60x + 60 - 60x + 60 = x2 - 1
=> 120 = x2 - 1
=> x2 = 121 => x = 11 (tm)
Vậy vận tốc thực cano là 11km/h

Đổi 20 phút = 1/3 h
Gọi x (km) là độ dài quãng đường AB (x > 0)
Thời gian khi đi xuôi dòng: x/30 (h)
Thời gian khi đi ngược dòng: x/24 (h)
Theo đề bài ta có phương trình:
x/24 - x/30 = 1/3
⇔ 5x - 4x = 40
⇔ x = 40 (nhận)
Vậy quãng đường AB dài 40 km

Gọi vận tốc thực của ca nô là: x (km/giờ) (ĐK: x > 0)
Thời gian đi xuôi dòng là: 9/(2 + x) (giờ)
Thời gian đi ngược dòng là: 8/(2 - x) (giờ)
=> Ta có PT:
\(\frac{8}{\left(2-x\right)}-\frac{9}{\left(2+x\right)}=\frac{1}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x=10\left(\text{TM}\right)\\x=-14\left(\text{loai}\right)\end{cases}}\)
Ta có: 15 phút =\(\frac{1}{4}\)giờ
Gọi vân tốc cano khi nước đứng yên là x,x>0 và tính bằng km/h
Đến đây, có 4 đại lượng biểu diễn là:
-Vận tốc cano xuôi dòng
-Vận tốc cano đi ngược dòng
-Thời gian cano đi xuôi dòng
-Thời gian cano đi ngược dòng
Các đại lượng này được thể hiện trong bảng sau
| Xuôi dòng | Ngược dòng | Chênh lệch | |
| Vận tốc | x+2 | x-2 | |
| Thời gian | \(\frac{9}{x+2}\) | \(\frac{8}{x-2}\) | \(\frac{8}{x-2}-\frac{9}{x+2}\) |
Nhìn vào bảng, ta dễ dàng lập phương trình:
\(\frac{8}{x-2}-\frac{9}{x+2}=\frac{1}{4}\)ĐK: \(x\ne\pm2\)
Mẫu chung là: 4(x-2)(x+2)
Quy đồng và khử mẫu, ta đưa về phương trình
x2+4x-140=0
<=> (x-10)(x+14)=0
<=> x1=10; x2=-14
Giá trị x2=-14 (loại) vì x>0
Vậy vận tốc thực của cano là 10km/h
*Trình bày bài bạn không cần đưa bảng vào nhé*

Gọi khoảng cách giữa AB là x(km).
Thời gian cano đi xuôi là: x/30(h)
Vận tốc cano ngược dòng là 20km
Vậy thời gian di ngược là x/20(h)
Thời gian xuôi ít hơn tg ngược 1h20'=4/3h nên ta có pt x/30+4/3=x/20
x = 80

ận tốc khi xuôi dòng là 36km/h (vx)
vận tốc dòng nước là 3 km/h
⇒ vận tốc thực của tàu là 36-3=33 km/h (vt)
gọi t là thời gian khi xuôi dòng ; t +\(\frac{2}{3}\)là thời gian khi đi ngươc dòng
ta có AB= vx.t =(vt-3)(t+2323)
⇔ 36t = 30t+20
⇔ 6t = 20
⇔ t=\(\frac{20}{6}\)(h)
⇒ AB=120 (km)
Gọi thời gian cano xuôi dòng là x (giờ)
Thời gian cano ngược dòng là \(x+1\) giờ
Quãng đường xuôi dòng: \(S=x\left(14+2\right)=16x\) (km)
Quãng đường ngược dòng: \(S=\left(x+1\right)\left(14-2\right)=12\left(x+1\right)\)
Do quãng đường xuôi dòng bằng quãng đường ngược dòng nên ta có pt:
\(16x=12\left(x+1\right)\Leftrightarrow x=3\)
Quãng đường: \(S=16.3=48\left(km\right)\)
Gọi x(km) là độ dài quãng sông AB ( x > 0 )
Vận tốc ca nô khi xuôi dòng là 14 + 2 = 16km/h
Thời gian ca nô xuôi dòng là x/16 giờ
Vận tốc ca nô khi ngược dòng là 14 - 2 = 12km/h
Thời gian ca nô ngược dòng là x/12 giờ
Theo bài ra ta có phương trình :
x/12 - x/16 = 1
<=> x( 1/12 - 1/16 ) = 1
<=> x.1/48 = 1
<=> x = 48 (tm)
Vậy độ dài quãng sông AB là 48km