Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 7 giờ 30 phút =15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 3
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 54/(x+3) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 54/(x-3) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
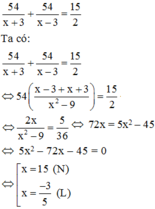
Vậy vận tốc thực của ca nô là 15 (km/h)
Đáp án: D

Đổi 8 giờ 6 phút = 81/10 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 2
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 2 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 2 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 72/(x+2) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 72/(x-2) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 8 giờ 6 phút nên ta có phương trình:
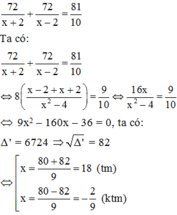
Vậy vận tốc thực của ca nô là 18 (km/h)
Đáp án: A

gọi vận tốc thực là x(x>4)km/h
vận tốc khi xuôi dòng là x+4 km/h
vận tốc khi ngược dòng là x-4 km/h
thời gian ca nô đi xuôi dòng là \(\dfrac{80}{x+4} \)h
thời gian ca nô đi ngược dòng là \(\dfrac{80}{x-4} \)h
vì tổng thời gian ca nô đi xuôi dòng và ngược dòng là 8h20p=\(\dfrac{25}{3} \)h
nên ta có pt \(\dfrac{80}{x+4} \)+\(\dfrac{80}{x-4} \)=\(\dfrac{25}{3} \)
giải pt x=-0.8 Ktm điều kiện
x= 20 TM
vậy vận tốc thực của ca nô là 20km/h

Gọi vận tốc thực của \(ca-nô\) là : \(x(km/giờ)(x>0)\)
\(\Rightarrow\) Vận tốc khi đi suôi dòng là :\(x+4(km/giờ)\)
\(\Rightarrow\)Thời gian đi xuôi dòng là : \(\dfrac{60}{x+4}\)\((km/giờ)\)
\(\Rightarrow\) Vận tốc đi ngược dòng là : \(x-4(km/giờ)\)
\(\Rightarrow\) Thời gian đi ngược dòng là : \(\dfrac{60}{x-4}\)\((km/giờ)\)
Theo bài ra ta có phương trình :
\(\dfrac{60}{x+4}+\dfrac{60}{x-4}=8\)
\(\Rightarrow60\left(x-4\right)+60\left(x+4\right)=8\left(x^2-16\right)\)
Giải ra ta được : \(\left\{{}\begin{matrix}x_1=16\left(tm\right)\\x_2=-1\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\) Vận tốc thực của \(ca-nô\) là \(16(km/giờ)\)

Gọi vận tốc riêng của cano là \(x\left(km/h\right),x>4\).
Vận tốc khi cano đi xuôi dòng là: \(x+4\left(km/h\right)\).
Thời gian cano đi xuôi dòng là: \(\frac{120}{x+4}\left(h\right)\).
Vận tốc khi cano đi ngược dòng là: \(x-4\left(km/h\right)\).
Thời gian cano đi ngược dòng là: \(\frac{96}{x-4}\left(h\right)\).
Ta có phương trình:
\(\frac{96}{x-4}-\frac{120}{x+4}=1\)
\(\Rightarrow96\left(x+4\right)-120\left(x-4\right)=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2+24x-880=0\)
\(\Leftrightarrow x=20\)(vì \(x>4\))
.

Gọi x (km/h) là vận tốc thực của ca nô (x > 2)
Giả sử đi từ A đến B là đi xuôi dòng
Vận tốc ca nô khi đi xuôi dòng: x + 2 (km/h)
Vận tốc ca nô khi đi ngược dòng: x - 2 (km/h)
Thời gian đi từ A đến B: 20/(x + 2) (h)
Thời gian đi từ B về A: 20/(x - 2) (h)
Đổi 4 giờ 40 phút = 14/3 (h)
Theo đề bài ta có phương trình:
20/(x + 2) + 20/(x - 2) = 14/3 - 1/2
⇔ 20/(x + 2) + 20/(x - 2) = 25/6
⇔ 6.20(x - 2) + 6.20(x + 2) = 25(x - 2)(x + 2)
⇔ 120x - 240 + 120x + 240 = 25(x² - 4)
⇔ 240x = 25x² - 100
⇔ 25x² - 240x - 100 = 0
⇔ 25x² - 250x + 10x - 100 = 0
⇔ (25x² - 250x) + (10x - 100) = 0
⇔ 25x(x - 10) + 10(x - 10) = 0
⇔ (x - 10)(25x + 10) = 0
⇔ x - 10 = 0 hoặc 25x + 10 = 0
*) x - 10 = 0
⇔ x = 10 (nhận)
*) 25x + 10 = 0
⇔ 25x = -10
⇔ x = -2/5 (loại)
Vậy vận tốc thực của ca nô là 10 km/h.
Đáp án A
Đổi 7 giờ 30 phút= 15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h; x > 3).
vận tốc của ca nô khi xuôi dòng sông từ A đến B là: x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là: x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là: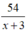 (h)
(h)
Thời gian của ca nô khi ngược dòng sông từ B về A là: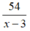 (h)
(h)
Do ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
Ta thấy chỉ có x = 15 thỏa mãn điều kiện x > 3.
Vậy vận tốc thực của ca nô là 15 (km/h).