Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 2d
Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o
...
Chúc bạn học tốt
câu 1d
+ ΔACI có BF//CI→ FC/FA=OI/AO
IΔCOI có AJ//CI (//BF)→ CI/AJ=OI/AO
→FC/FA=CI/AJ

a)
Xét tam giác ABF và tam giác ACB có:
BAC chung
ABF = ACB (gt)
=> Tam giác ABF ~ Tam giác ACB (g - g)
=> \(\dfrac{\text{AF}}{AB}=\dfrac{AB}{AC}\)
=> \(\dfrac{\text{AF}}{4}=\dfrac{4}{8}\)
=> AF = 2 (cm)
Ta có:
AF + FC = AC
2 + FC = 8
FC = 6 (cm)
b)
D là trung điểm của BC (AD là đường trung tuyến của tam giác ABC)
=> \(DC=\dfrac{1}{2}BC\)
Kẻ đường cao AH (H \(\in\) BC)
Ta có: \(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{\dfrac{1}{2}\times AH\times AB}{\dfrac{1}{2}\times AH\times DC}=\dfrac{AB}{\dfrac{1}{2}AB}=2\)
=> SABC = 2SADC
c)
Tam giác CKA có OF // KA (gt) nên theo định lý Talet
=> \(\dfrac{FC}{FA}=\dfrac{OC}{OK}\left(1\right)\)
Tam giác OCI có KA // CI (gt) nên theo hệ quả của định lý Talet
=> \(\dfrac{OC}{OK}=\dfrac{CI}{KA}\left(2\right)\)
(1) và (2)
=> \(\dfrac{FC}{FA}=\dfrac{CI}{KA}\)
d)
Tam giác DCI có CI // BO nên theo hệ quả của định lý Talet
=> \(\dfrac{DB}{DC}=\dfrac{BO}{CI}\)
Tam giác EBO có AK // BI nên theo hệ quả của định lý Talet
=> \(\dfrac{EA}{EB}=\dfrac{AK}{BO}\)
Ta có:
\(\dfrac{DB}{DC}\times\dfrac{EA}{EB}\times\dfrac{FC}{FA}=\dfrac{BO}{CI}\times\dfrac{AK}{BO}\times\dfrac{CI}{KA}=1\)


a) ΔADB và ΔABC vuông có ∠B chung ∠ ΔADB ∼ ΔCAB (g.g)
b) Vì ∠B = 2∠C (gt) ∠ ∠B1 = ∠B2 = ∠C
Do đó hai tam giác vuông ABE và ACB đồng dạng (g.g)
![]()
c) Ta có ΔADB ∼ ΔCAB (cmt)
![]()
Theo tính chất đường phân giác ta có :

d) Ta có AB = 2BD (gt)
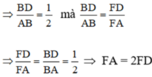
![]()


a.Xét \(\Delta ADB\)và \(\Delta CAB\)có:
\(\widehat{ADB}=\widehat{CAB}=90^o\)
\(\widehat{ABC}\)chung
\(\Rightarrow\Delta ADB~\Delta CAB\left(g.g\right)\)
b.Kí hiệu: \(\widehat{ABE}=\widehat{B_1};\widehat{EBC}=\widehat{B_2}\)
Ta có:\(\widehat{B}=2\widehat{C}\)
\(\Rightarrow\widehat{B_1}=\widehat{B_2}=\widehat{C}\)
Vì \(\Delta ADB~\Delta CAB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AC}{AB}\)
\(\Rightarrow AB^2=AE.AC\)
c.Ta có:\(\Delta ABB~\Delta CAB\left(g.g\right)\)(cm câu a)
\(\Rightarrow\frac{BA}{BC}=\frac{BD}{AB}\)
Theo t/c đường p/g ta có: \(\frac{BA}{BC}=\frac{EA}{EC}\)và \(\frac{BD}{BA}=\frac{FD}{FA}\)
\(\Rightarrow\frac{FD}{FA}=\frac{EA}{EC}\left(đpcm\right)\)
d.Ta có:\(AB=2BD\left(gt\right)\)
\(\Rightarrow\frac{BD}{AB}=\frac{1}{2}\)
Mà \(\frac{BD}{AB}=\frac{FD}{FA}\)(câu c)
\(\Rightarrow\frac{BD}{AB}=\frac{FD}{FA}=\frac{1}{2}\)
\(\Rightarrow FA=2FD\)
Mà \(S_{ABC}=\frac{1}{2}BC.AD\)
và \(S_{BFC}=\frac{1}{2}BC.FD\)
\(\Rightarrow S_{ABC}=3S_{BFC}\left(đpcm\right)\)

a)
xét tam giác ABD và tam giác ACB có:
góc A chung;góc ABD=góc ACB =>tam giác ABD đồng dạng tam giác ACB(đpcm)
=>AD/AB=AB/AC =>AD=AB*AB/AC=2*2/4=1.vậy AD=1cm
ta lại có
AC=AD+DC =>DC=AC-AD=4-1=3cm.vậy DC=3cm
b)xét tm giác ABH vuông tại H và tam giác ADK vuông tại K có:
góc ABH=góc ADK( do tam giác ABC đồng dạng tam giác ABD,cmt)
=>tam giác ABH đồng dạng tam giác ADK(g-g)
=>AB/AD=AH/AK=BH/DK
mà AB/AD=2/1
=>AB/AD=AH/AK=BH/DK=2/1
mặt khác:
diện tích tam giác ABH/diện tích tam giác ADK=k2
=(2/1)2=4/1
=>diện tích tam giác ABH=4 diện tích tam giác ADK(đpcm)
(câu b mk cũng kg bit đúng kg nữa,mk làm theo suy nghĩ của mk,có j sai,b góp ý giúp mk nhé)

a/ Xét tg HBA và tg ABC, có:
góc BHA = góc BAC = 90 độ
góc B chung
Suyra: tg HBA đồng dạng với tg ABC (g-g)
b/ Ta có tg ABC vuông tại A:
\(BC^2=AC^2+AB^2\)
\(BC^2=8^2+6^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\)(cm)
Ta có: \(\frac{HA}{AC}=\frac{BA}{BC}\)(tg HBA đồng dạng với tg ABC)
\(\Rightarrow\frac{HA}{8}=\frac{6}{10}\)
\(\Rightarrow HA=\frac{8.6}{10}=4,8\left(cm\right)\)
a) xét tam giác ABF zà tam giác ACB có
BAC chung
ABF= ACB (gt)
=> tam giác ABF= tam giác ACB (g.g)
\(=>\frac{AF}{AB}=\frac{AB}{AC}=>\frac{AF}{AB}=\frac{4}{8}=>AF=2\)
ta có AF+FC=AC
=> 2+FC=8
=>FC=6
b) D là trung điểm của BC ( AD là trung tuyến của tam giác ABC
=>\(DC=\frac{1}{2}BC\)
kẻ đường cao AH
ta có \(\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.AB}{\frac{1}{2}.AH.DC}=\frac{AB}{DC}=\frac{AB}{\frac{1}{2}AB}=2\)
\(=>S_{ABC}=2S_{ADC}\)
c) tam giác CKA có OF//KA nên theo đ/l ta lét có
\(\frac{FC}{FA}=\frac{OC}{OK}\left(1\right)\)
tam giác OCI có KA//CI nên theo hệ quả đ/l ta lét ta có
\(\frac{OC}{OK}=\frac{CI}{KA}\left(2\right)\)
từ 1 zà 2 \(=>\frac{FC}{FA}=\frac{CI}{KA}\)
lại câu c nhé
c) ta có Cx//BF nên theo đ.l ta lét ta đc
\(\frac{FC}{FA}=\frac{OI}{OA}\)
Cx//AY( hệ quả ta lét )=>\(\frac{OI}{OA}=\frac{CJ}{JA}\Leftrightarrow\frac{FC}{FA}=\frac{CI}{JA}\)
tương tự ta có
\(\frac{DB}{DC}=\frac{BO}{CI}\left(hệ\right)quả\)
\(\frac{FC}{FA}=\frac{CI}{JA}\left(cmt\right)\)
mặt khác Ay//FB ta có
\(\frac{EA}{EB}=\frac{JA}{BO}=>\frac{DB}{DC}.\frac{FC}{FA}.\frac{EA}{EB}=\frac{BO}{CI}.\frac{CI}{JA}.\frac{JA}{BO}=1\)(dpcm)