K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
0P
1
13 tháng 6 2023
Δ vuông góc d3
=>Δ: x+2y+c=0
Tọa độ giao của(d1) và (d2) là;
x+3y=1 và x-3y=5
=>x=3 và y=-2/3
Thay x=3 và y=-2/3 vào Δ, ta được:
c+3-4/3=0
=>c=-5/3
22 tháng 12 2022
=>2x-2y=1 và 2x+2y=-1
=>4x=0 và x-y=1/2
=>x=0 và y=0-1/2=-1/2
22 tháng 12 2022
Có cách bấm máy tính 570vn plus không ạ em cần biết cách bấm máy tính ạ
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
17.
\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(luôn-đúng\right)\\\Delta'=\left(2m-1\right)^2-\left(3m^2-2m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2-2m-3< 0\)
\(\Leftrightarrow-1< m< 3\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
18.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{2\sqrt{5}}{5}\)
\(tan\left(x+\dfrac{\pi}{4}\right)=\dfrac{tanx+tan\dfrac{\pi}{4}}{1-tanx.tan\dfrac{\pi}{4}}=\dfrac{\dfrac{2\sqrt{5}}{5}+1}{1-\dfrac{2\sqrt{5}}{5}.1}=9+4\sqrt{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
19.
\(a^2=b^2+c^2+bc\Rightarrow b^2+c^2-a^2=-bc\)
\(\Rightarrow cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{-bc}{2bc}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)
20.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
\(d\left(I;\Delta\right)=\dfrac{\left|2-1-3\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}IH=d\left(I;\Delta\right)\\AH=\dfrac{1}{2}AB\end{matrix}\right.\)
Áp dụng định lý Pitago trong tam giác vuông IAH:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+AH^2\)
\(\Rightarrow AH=\sqrt{2}\Rightarrow AB=2AH=2\sqrt{2}\)
KH
31 tháng 8 2019
Hi bạn! Xin được làm quen =)
CTV = Cộng tác viên
Để làm CTV thì bạn cần có điểm giá trị từ 300GP trở lên hoặc 200GP với mỗi môn, hoạt động tích cực trên diễn đàn hoc24
Về vấn đề bạn đề cập đến thì lí do là:
+ CTV tuyển trong 1 thời gian nhất định, có nhiều bạn nhiều GP nhưng lại nghỉ ngay lúc đó nên k đăng kí được
+ Hoặc các bạn nhiều GP ấy là từ những nhiệm kì trước đạt được, trong khoảng thời gian trước 3 tháng hoạt động ít hoặc k hoạt động
→ Dẫn đến vấn đề bạn đề cập
31 tháng 8 2019
Những người có điểm Gp trên 200 đối với 1 môn thì được làm CTV , 300GP đối với tổng các môn
Những người có ít GP được làm CTV , 1 là giáo viên gì đó k rõ cho lắm
Còn những người cao GP mà chưa làm CTV nghĩa là họ chưa đăng kí CTV hoặc lúc thầy tuyển CTV thì họ chưa đủ điểm
Đối với những người khoảng trên 200GP mà được CTV là họ đã được 200GP với 1 môn và đã đăng kí làm CTV
Đăng kí làm CTV đối vời từng kì thầy sẽ tuyển
V
1
31 tháng 8 2021
Ta có:
\(2011^3\equiv1\left(mod7\right)\Rightarrow\left(2011^3\right)^{668}\equiv1^{668}\equiv1\left(mod7\right)\)
Lại có:
\(1468^3\equiv-1\left(mod7\right)\Rightarrow\left(1468^3\right)^{669}\equiv\left(-1\right)^{669}\equiv-1\left(mod7\right)\)
Do đó:
\(2011^{2004}+1468^{2007}\equiv1+\left(-1\right)\equiv0\left(mod7\right)\)
Vậy ta có đpcm
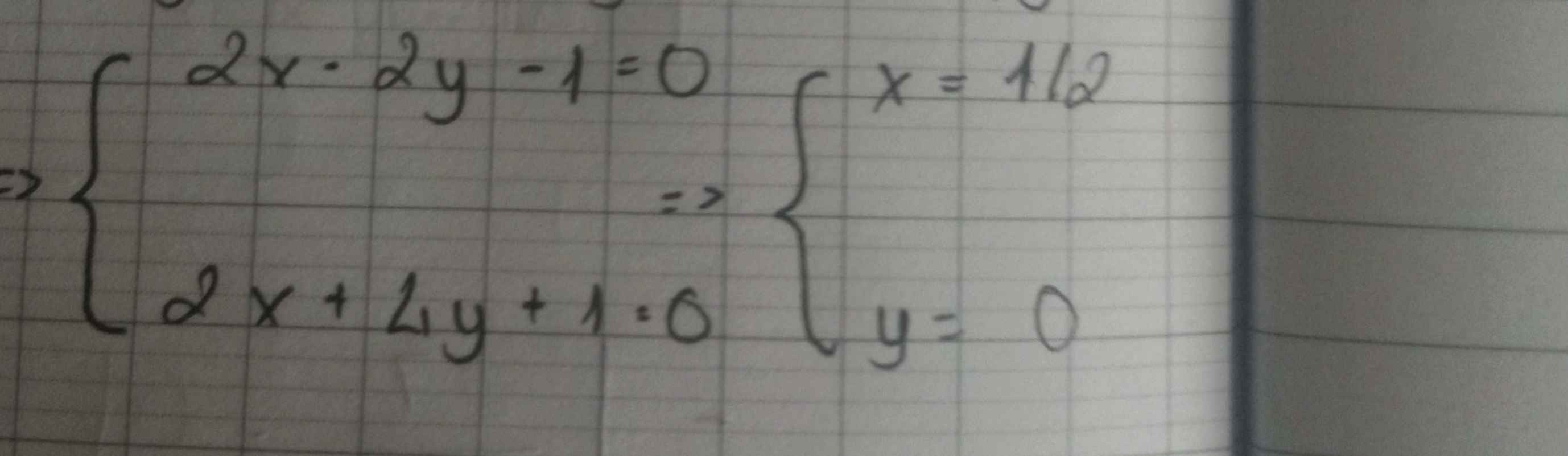
\(f\left(x\right)=x^2-\left(2m-1\right)x-2\sqrt{x}+m^2-2m\)
1) đk: \(x\ge0\)
Thay m=2 vào \(f\left(x\right)=0\) ta được: \(x^2-3x-2\sqrt{x}=0\)
\(\Leftrightarrow\)\(\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\\\sqrt{x}+1=0\left(vn\right)\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)(tm)
2) Thay m=6 vào f(x) ta được:
\(f\left(x\right)=x^2-11x-2\sqrt{x}+24\)
\(f\left(x\right)\le0\) \(\Leftrightarrow x^2-11x-2\sqrt{x}+24\le0\) (bước này coi \(\sqrt{x}\) là nghiệm thì sẽ trở thành bpt
bậc 4 ,bấm máy tính sẽ tìm được nghiệm)
\(\Leftrightarrow\)\(\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}-\dfrac{-1+\sqrt{17}}{2}\right)\left(\sqrt{x}+\dfrac{1+\sqrt{17}}{2}\right)\le0\)
mà \(\sqrt{x}\ge0\) \(\Rightarrow\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}+\dfrac{1+\sqrt{17}}{2}>0\end{matrix}\right.\)
bpt \(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}-\dfrac{-1+\sqrt{17}}{2}\right)\le0\)
\(\Leftrightarrow\sqrt{x}\in\left[\dfrac{-1+\sqrt{17}}{2};3\right]\)
\(\Leftrightarrow x\in\left[\dfrac{9-\sqrt{17}}{2};9\right]\)