
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo phương thức đã học; ta có:
(a . b)= ƯCLN (a,b) .BCNN (a,b)
=> 1350 = ƯCLN(a,b) . 90
=.> ƯCLN (a,b) =1350 :90 = 15
Nhớ k cho mình nhé,như lời hứa

31 - [ 26 - ( 209 + 35 ) ]
= 31 - ( 26 - 344 )
=31 - ( -318)
= 31 + 318 ( trừ trừ thành cộng nha )
= 349
31-(26-(209+35)=31-
hok tốt
k cho mik
kb nữa nhé

`1)a)5/9 + (-2)/9 = (5+(-2))/9 = 3/9 = 1/3`
`b)(-5)/9 : 10/3 = (-5)/9 . 3/10 = (-5.3)/(9.10) = (-15)/90 = (-1)/6`
`c)(-5)/4 + (-1)/3 +5/4 = (-5/4 + 5/4) + (-1)/3 = 0 + (-1)/3 = -1/3`
`d)(-2)/7 . 5/6 + (-2)/7 . 5/6 = (-2)/7 . ( 5/6 + 5/6 ) = (-2)/7 . 10/6 = (-2)/7 . 5/3 = (-2.5)/(7.3) = (-10)/24 = (-5)/12`
Gì đây mới câu 1 thôi, Còn câu 2,3,4,5 trên bài đâu, giải nhanh đây trước 14h05 trong ngày hôm nay nha.


Ta có : \(12a+7b=64\)
Do \(64⋮4,12a⋮4\) \(\Rightarrow7b⋮4\) mà \(\left(7,4\right)=1\)
\(\Rightarrow b⋮4\) (1)
Từ giả thiết \(\Rightarrow7b\le64\) \(\Leftrightarrow b\le9\) kết hợp với (1)
\(\Rightarrow b\in\left\{4,8\right\}\)
+) Với \(b=4\) thì : \(12a+7\cdot4=64\)
\(\Leftrightarrow12a=36\)
\(\Leftrightarrow a=3\) ( thỏa mãn )
+) Với \(b=8\) thì \(12a+7\cdot8=64\)
\(\Leftrightarrow12a=8\)
\(\Leftrightarrow a=\frac{8}{12}\) ( loại )
Vậy : \(\left(a,b\right)=\left(3,4\right)\)
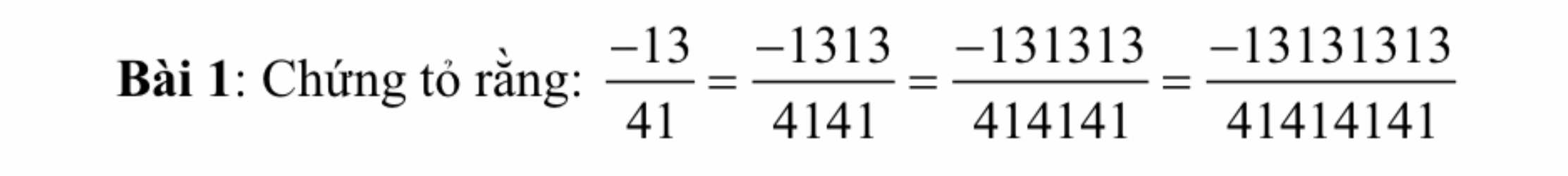


\(-\dfrac{13}{41}=\dfrac{-13.101}{41.101}=\dfrac{-1313}{4141}\) (1)
\(\dfrac{-13}{41}=\dfrac{-13.10101}{41.10101}=\dfrac{-131313}{414141}\)(2)
\(\dfrac{-13}{41}=\dfrac{-13.1010101}{41.1010101}=\dfrac{-13131313}{41414141}\)(3)
từ (1)(2)(3)=> \(\dfrac{-13}{41}=\dfrac{-1313}{4141}=\dfrac{-131313}{414141}=\dfrac{-13131313}{41414141}\)