TT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 9 2021
x ∈ {năng lượng gió, năng lượng mặt trời, năng lượng địa nhiệt}
y ∈ {năng lượng gió, năng lượng mặt trời}
VM
1
1 tháng 3 2022
a: Các cặp điểm cùng phía với điểm I và C;K; C;B; K;B
b: Tia đối của tia CK là tia CA
c: AI=1cm
=>AC=2cm
=>CB=6cm
=>KB=3cm
8 tháng 1 2017
1000 ! .( 456 . 789789 - 789 . 456456 )
= 1000 ! x ( 456 x 789 x 1001 - 789 x 456 x 1001 )
= 1000 ! x 0 = 0
8 tháng 1 2017
1000 ! .( 456 . 789789 - 789 . 456456 )
= 1000 ! x ( 456 x 789 x 1001 - 789 x 456 x 1001 )
= 1000 ! x 0 = 0
DN
3
5 tháng 5 2021
Lời giải chi tiết
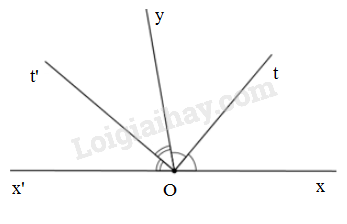
Hai góc xOyxOy và x′Oyx′Oy là hai góc kề bù nên ˆxOy+ˆx′Oy=1800xOy^+x′Oy^=1800 mà ˆxOy=1000xOy^=1000 nên ˆx′Oy=1800−ˆxOyx′Oy^=1800−xOy^=1800−1000=800=1800−1000=800
Vì OtOt là tia phân giác của góc xOyxOy nên ˆxOt=ˆtOy=ˆxOy2xOt^=tOy^=xOy^2=10002=500=10002=500
Vì Ot′Ot′ là tia phân giác của góc x′Oyx′Oy nên ˆx′Ot′=ˆt′Oyx′Ot′^=t′Oy^=ˆx′Oy2=8002=400=x′Oy^2=8002=400
+ Góc x′Otx′Ot và góc xOtxOt là hai góc kề bù nên ˆx′Ot+ˆxOt=1800x′Ot^+xOt^=1800
Suy ra ˆx′Ot=1800−ˆxOt=1800−500=1300x′Ot^=1800−xOt^=1800−500=1300
+ Góc xOt′xOt′ và góc x′Ot′x′Ot′ là hai góc kề bù nên ˆxOt′+ˆx′Ot′=1800xOt′^+x′Ot′^=1800
Suy ra ˆxOt′=1800−ˆx′Ot′=1800−400=1400xOt′^=1800−x′Ot′^=1800−400=1400
+ Vì tia Ot′Ot′ nằm giữa hai tia Ox′Ox′ và Oy,Oy, tia OtOt nằm giữa hai tia OxOx và OyOy
Lại có hai góc xOyxOy và x′Oyx′Oy là hai góc kề bù nên tia OyOy nằm giữa hai tia OxOx và Ox′Ox′
Suy ra tia OyOy nằm giữa hai tia OtOt và Ot′Ot′
Do đó ˆyOt′+ˆyOt=ˆt′OtyOt′^+yOt^=t′Ot^
Suy ra ˆt′Ot=500+400=900t′Ot^=500+400=900
AH
Akai Haruma
Giáo viên
29 tháng 1 2022
Bài 4:
$A+2=1+2+2^2+2^3+...+2^{11}$
$=(1+2)+(2^2+2^3)+....+(2^{10}+2^{11})$
$=(1+2)+2^2(1+2)+....+2^{10}(1+2)$
$=(1+2)(1+2^2+....+2^{10})$
$=3(1+2^2+...+2^{10})\vdots 3$
Vậy $A+2\vdots 3$ nên $A$ không chia hết cho $3$
AH
Akai Haruma
Giáo viên
29 tháng 1 2022
Bài 5:
$n^2+n+1=n(n+1)+1$
Vì $n,n+1$ là hai số tự nhiên liên tiếp nên sẽ tồn tại một số chẵn và 1 số lẻ
$\Rightarrow n(n+1)$ chẵn
$\Rightarrow n^2+n+1=n(n+1)+1$ lẻ (điều phải chứng minh)
8 tháng 1 2016
chưa đủ bạn ơi còn nhiều số nữa hãy gắng suy nghĩ giúp mình đi
a) Theo giả thiết: \(\widehat{x0y}=180^{0}\)
\(\Rightarrow\)\(\widehat{zOt}=180^{0}-30^{0}-75^{0}=75^{0}\)
b)Theo câu a) \(\widehat{tOy}=\widehat{z0t}=75^{0}\)
\(\Rightarrow\)Ot là tia phân giác(đpcm)