
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-23,8\cdot41,9-23,8\cdot67,2+23,8\cdot9,1\)
\(=-23,8\cdot\left(41,9+67,2-9,1\right)\)
\(=-23,8\cdot100\)
\(=-2380\)


Ta có:
x.(x+y+z)+y.(x+y+z)+z.(x+y+z)=(x+y+z)(x+y+z)=\(\left(x+y+z\right)^2=3+9+4=16\)
Suy ra x+y+z có thể bằng 4 hoặc -4
TH1: x+y+z=4
\(\Rightarrow x=\frac{3}{4};y=\frac{9}{4};z=1\)
TH2: x+y+z=-4
\(\Rightarrow x=\frac{-3}{4};y=\frac{-9}{4};z=-1\)

Ta có :
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}=\left(\frac{a+b+c}{b+c+d}\right)^3\) (1)
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\frac{a}{d}\) (2)
Từ (1) và (2) suy ra điều phải chứng minh
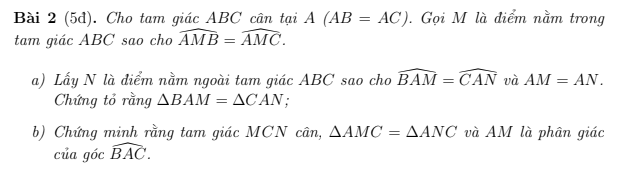

 Mọi người giải giúp mình câu 6
Mọi người giải giúp mình câu 6