K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
O
7 tháng 4 2022
a) \(x-3=0\)
\(\Leftrightarrow\) \(x=0+3\)
\(\Leftrightarrow\) \(x=3\)
b) \(2x+6=0\)
\(\Leftrightarrow\) \(2x=0-6\)
\(\Leftrightarrow2x=-6\)
\(\Leftrightarrow x=-3\)
c) \(2x+3=x+9\)
\(\Leftrightarrow2x+3-x=9\)
\(\Leftrightarrow x+3=9\)
\(\Leftrightarrow x=9-3\)
\(\Leftrightarrow x=6\)
d) \(\left(x-4\right)\left(2x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\2x+4+\left(-4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
LM
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
3.
Gọi vận tốc xe thứ nhất là x (km/h) với x>0
Vận tốc xe thứ hai là: \(1,2x\) (km/h)
Thời gian xe thứ nhất đi hết quãng đường AB: \(\dfrac{120}{x}\) giờ
Thời gian xe thứ hai đi hết quãng đường AB: \(\dfrac{120}{1,2x}=\dfrac{100}{x}\) giờ
Do xe thứ hai đến sớm hơn xe thứ nhất là 30 phút =1/2 giờ nên ta có pt:
\(\dfrac{120}{x}-\dfrac{100}{x}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{20}{x}=\dfrac{1}{2}\Rightarrow x=40\) (km/h)
Vậy vận tốc xe thứ nhất là 40 km/h, xe thứ hai là \(40\times1,2=48\) (km/h)
4.
Áp dụng định lý phân giác ta có:
\(\dfrac{IE}{IF}=\dfrac{DE}{DF}=\dfrac{6}{10}=\dfrac{4}{5}\)
19 tháng 8 2021
a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=\left(3x^2-6x+3\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-5+20x\)
\(=-30\)
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+\left(4x^2+4x+1\right)+\left(x^3-3x^2+9x+3x^2-9x+27\right)-1\)
\(=27\)
19 tháng 8 2021
a: Ta có: \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
b: Ta có: \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
=27
18 tháng 6 2019
Ta có : y=−13x3+(m−1)x2+(m+3)x−4y=−13x3+(m−1)x2+(m+3)x−4
Có y′=−x2+2(m−1)x+(m+3)y′=−x2+2(m−1)x+(m+3).
Để hàm số nghịch biến trên (0;3)(0;3) thì f′(x)<0∀x∈(0;3)f′(x)<0∀x∈(0;3) nghĩa là :
−x2+2(m−1)x+m+3<0⇔m<x2+2x−32x+1−x2+2(m−1)x+m+3<0⇔m<x2+2x−32x+1 với mọi x∈(0;3)x∈(0;3)
Đến đây ta chỉ việc tìm cực tiểu của hàm số f(x)=x2+2x−32x+1f(x)=x2+2x−32x+1 trên (0;3)(0;3).
Dễ dàng chứng minh f(x)f(x) đồng biến nên f(x)>f(0)=−3f(x)>f(0)=−3.
Vậy m≤−3m≤−3.
------------------------------------------
P/S:Ko chắc 
21 tháng 12 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
ML
0
7 tháng 12 2021
Bài 1:
\(a,=\dfrac{3x-3+4x+2+1-5x}{6x}=\dfrac{2x}{6x}=\dfrac{1}{3}\\ b,=\dfrac{x+y+2x-2y-3}{\left(x-y\right)\left(x+y\right)}=\dfrac{3x-y-3}{\left(x-y\right)\left(x+y\right)}\\ c,=\dfrac{4x-8-3x-6+12}{\left(x-2\right)\left(x+2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)
Bài 2:
\(a,A=\dfrac{x-1+x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x-1}=\dfrac{1}{11-1}=\dfrac{1}{10}\\ b,B=\dfrac{x^2+2x+1-x^2-2x}{x\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x\left(x^2-1\right)}=\dfrac{1}{\left(-\dfrac{1}{3}\right)\left(\dfrac{1}{9}-1\right)}=\dfrac{27}{8}\)
Bài 3:
\(a,=\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{3+x}+\dfrac{1}{x+3}=\dfrac{1}{x}\)
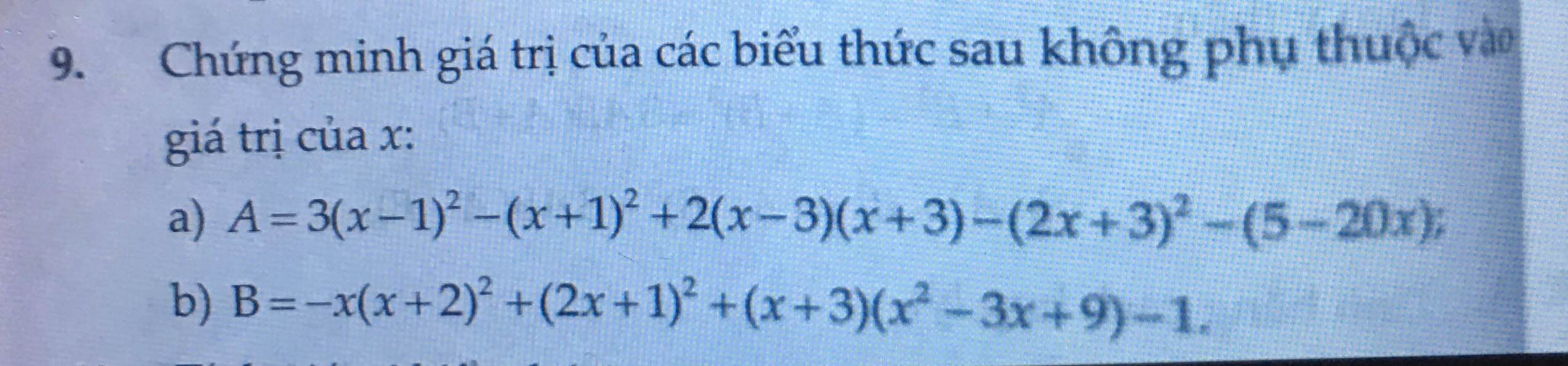
Bài 2:
a: \(201^3=8120601\)
b: \(199^3=7880599\)
c: \(52^3-8=140600\)
d: \(23^3-27=12140\)
e: \(99^3=970299\)
f: \(62\cdot58=3596\)
Bài 1:
a: \(\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=4x^2+4xy+y^2-y^2+4xy-4x^2\)
=8xy
b: \(\left(5x+5\right)^2+10\cdot\left(x-3\right)\left(x+1\right)+x^2-6x+9\)
\(=\left(5x+5\right)^2+2\cdot\left(5x+5\right)\cdot\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(6x+2\right)^2\)
\(=36x^2+24x+4\)
c: \(\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=x^3-3x^2y+3xy^2-y^3+3x^2y-3xy^2\)
\(=x^3-y^3\)
d: \(\left(1-2x\right)\left(1+2x+4x^2\right)+8\left(x-1\right)\left(x^2+x+1\right)\)
\(=1-8x^3+8\left(x^3-1\right)\)
\(=1-8x^3+8x^3-8\)
=-7