
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Xét tam giác vuông $DEM$ và $DFN$ có:
$DE=DF$ (do $DEF$ là tgc tại $D$)
$\widehat{D}$ chung
$\Rightarrow \triangle DEM=\triangle DFN$ (ch-gn)
$\Rightarrow DM=DN$
Xét tam giác vuông $DNO$ và $DMO$ có:
$DO$ chung
$DM=DN$
$\Rightarrow \triangle DNO=\triangle DMO$ (ch-cgv)
$\Rightarrow \widehat{NDO}=\widehat{MDO}$ hay $\widehat{EDI}=\widehat{FDI}$
Xét tam giác $DEI$ và $DFI$ có:
$DI$ chung
$DE=DF$
$\widehat{EDI}=\widehat{FDI}$
$\Rightarrow \triangle DEI=\triangle DFI$ (c.g.c)
$\Rightarrow EI=FI$ (đpcm)


Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: HB=HC
=>AH là đường trung tuyến
=>AH là đường trung trực
=>AH là phân giác

Bạn ơi chứng minh nhỏ hơn hoặc bằng 0 nhé
\(=-y^{2018}-\left(x^2-x+1\right)\)
\(=-y^{2018}-\left(x+1\right)^2\)
Vì \(\hept{\begin{cases}-y^{2018}\le0;\forall x,y\\-\left(x+1\right)^2\le0;\forall x,y\end{cases}}\)
\(\Rightarrow-y^{2018}-\left(x+1\right)^2\le0;\forall x,y\left(đpcm\right)\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BC=6cm
nên BM=3cm
=>AM=4cm
d: Xét ΔABC cân tại A có AM là đường cao
nên AM là phân giác của góc BAC
Xét ΔABC có
AM là đường phân giác
BI là đường phân giác
AM cắt BI tại I
Do đó: CI là tia phân giác của góc ACB
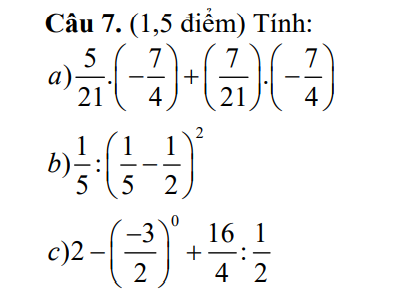


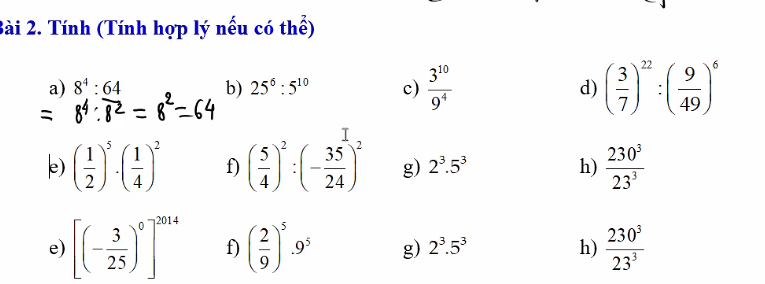


 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
\(=-\dfrac{7}{4}.(\dfrac{5}{21}+\dfrac{7}{21})\)
\(=-\dfrac{7}{4}.\dfrac{12}{21}\)
\(=-1\)
a) \(=\left(-\dfrac{7}{4}\right).\left(\dfrac{5}{21}+\dfrac{7}{21}\right)=\left(-\dfrac{7}{4}\right).\dfrac{4}{7}=-1\)
b) \(=\dfrac{1}{5}:\left(\dfrac{-3}{10}\right)^2=\dfrac{1}{5}.\dfrac{100}{9}=\dfrac{20}{9}\)
c) \(=2-0+4.2=2+8=10\)