
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
\(P=\dfrac{4x^2-2x+7}{2x-1}=\dfrac{2x\left(2x-1\right)+7}{2x-1}=2x+\dfrac{7}{2x-1}\in Z\\ \Leftrightarrow2x-1\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow x\in\left\{-3;0;1;4\right\}\\ Q=\dfrac{4x^2-2x+3}{2x-1}=\dfrac{2x\left(2x-1\right)+3}{2x-1}=2x+\dfrac{3}{2x-1}\in Z\\ \Leftrightarrow2x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-1;0;1;2\right\}\)
Bài 5:
\(M=\dfrac{\left(5x-1\right)\left(5x+1\right)}{1-5x}+\dfrac{\left(y-3\right)\left(5x+1\right)}{y-3}=-\left(5x+1\right)+5x+1=0\)
Bài 6:
\(VT=\dfrac{a\left(a+3b\right)}{\left(a+3b\right)\left(a-3b\right)}-\dfrac{\left(2a+b\right)\left(a-3b\right)}{\left(a-3b\right)^2}=\dfrac{a}{a-3b}-\dfrac{2a+b}{a-3b}=\dfrac{-a-b}{a-3b}\)
\(VP=\dfrac{\left(a+b\right)\left(a+c\right)}{\left(a+c\right)\left(3b-a\right)}=\dfrac{a+b}{3b-a}=\dfrac{-a-b}{a-3b}\)
Vậy ta đc đpcm

1.
a.
\(n^2+7n+1=k^2\Rightarrow4n^2+28n+4=4k^2\)
\(\Leftrightarrow\left(2n+7\right)^2-45=\left(2k\right)^2\)
\(\Leftrightarrow\left(2n-2k+7\right)\left(2n+2k+7\right)=45\)
Phương trình ước số cơ bản
b.
\(a^3b^3+b^3-3ab^2=-1\)
\(\Leftrightarrow a^3+1-\dfrac{3a}{b}=-\dfrac{1}{b^3}\)
\(\Leftrightarrow a^3+\dfrac{1}{b^3}+1-\dfrac{3a}{b}=0\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x^3+y^3+1-3xy=0\)
\(\Leftrightarrow\left(x+y\right)^3+1-3xy\left(x+y\right)-3xy=0\)
\(\Leftrightarrow\left(x+y+1\right)\left(x^2+y^2+1-xy-x-y\right)=0\)
\(\Leftrightarrow x+y+1=0\)
\(\Rightarrow P=a+\dfrac{1}{b}=x+y=-1\)
2.
a.
\(a+b+\dfrac{1}{a}+\dfrac{1}{b}=\left(\dfrac{a}{4}+\dfrac{1}{a}\right)+\left(\dfrac{b}{4}+\dfrac{1}{b}\right)+\dfrac{3}{4}\left(a+b\right)\)
\(\ge2\sqrt{\dfrac{a}{4a}}+2\sqrt{\dfrac{b}{4b}}+\dfrac{3}{4}.4=5\) (đpcm)
Dấu "=" xảy ra khi \(a=b=2\)

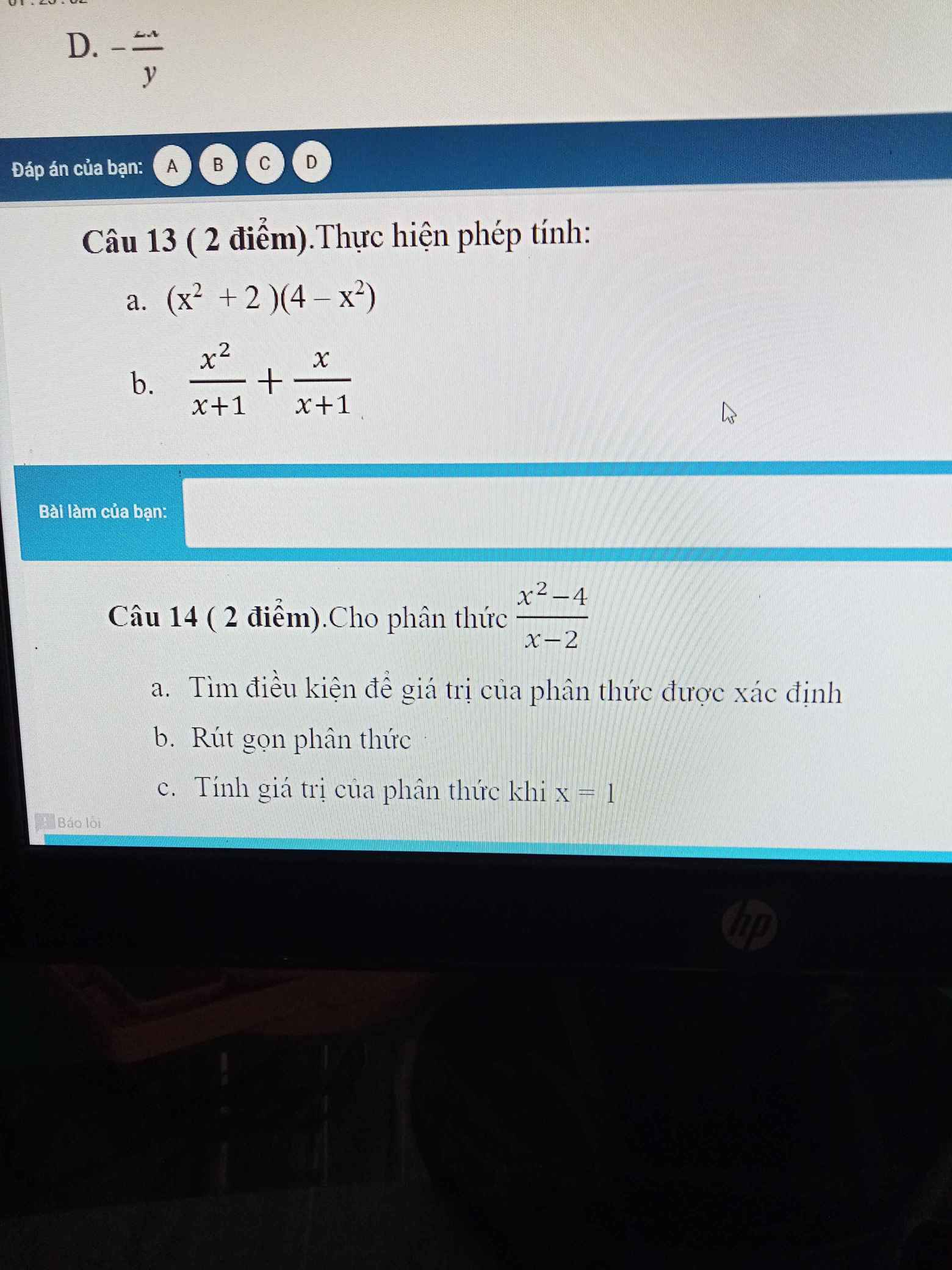
Câu 14;
a: ĐKXĐ: x<>2
b: \(\dfrac{x^2-4}{x-2}=x+2\)
c: Thay x=1 vào x+2, ta được:
x+2=1+2=3

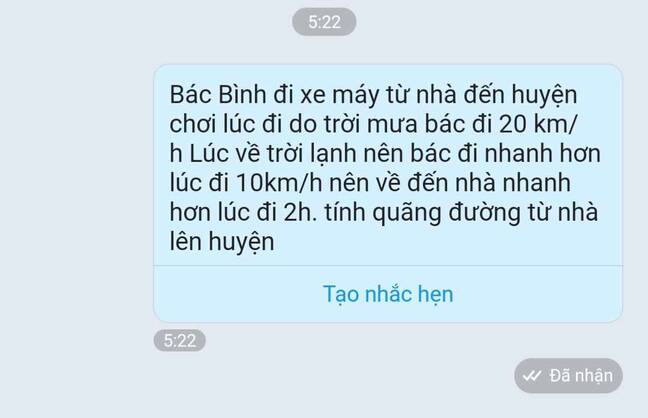
Gọi \(x\left(km\right)\) là quãng đường từ nhà bác Bình lên huyện \(\left(x>0\right)\)
Vì vận tốc lúc đi là 20km/h nên thời gian lúc đi là \(\dfrac{x}{20}\left(h\right)\)
Vận tốc lúc về nhanh hơn so với lúc đi là 10km/h (tức vận tốc lúc về là 30km/h) nên thời gian lúc về là \(\dfrac{x}{30}\left(h\right)\)
Vì thời gian về nhanh hơn thời gian đi là 2 giờ nên ta có pt \(\dfrac{x}{20}-\dfrac{x}{30}=2\Leftrightarrow\dfrac{3x-2x}{60}=2\Leftrightarrow\dfrac{x}{60}=2\Rightarrow x=120\) (nhận)
Vậy quãng đường từ nhà bác Bình đến huyện là 120km.

-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

Bài 1:
a: \(\Leftrightarrow x^2-3x+5x-x^2+8=0\)
=>2x=-8
hay x=-4
b: \(\Leftrightarrow\left(x+4\right)\left(3-x\right)=0\)
hay \(x\in\left\{-4;3\right\}\)
Bài 2:
\(\Leftrightarrow x^4-x^3+5x^2-5x^2+5x-25+a+25⋮x^2-x+5\)
=>a+25=0
hay a=-25

\(18,\\ \dfrac{1-9x^2}{x^2+4x}:\dfrac{2-6x}{3x}\left(x\ne0;x\ne-4;x\ne\dfrac{1}{3}\right)\\ =\dfrac{\left(1-3x\right)\left(1+3x\right)}{x\left(x+4\right)}\cdot\dfrac{3x}{2\left(1-3x\right)}=\dfrac{3\left(1+3x\right)}{2\left(x+4\right)}\\ \dfrac{27-x^3}{5x+10}:\dfrac{x-3}{3x+6}\left(x\ne-2;x\ne3\right)=\dfrac{\left(3-x\right)\left(x^2+3x+9\right)}{5\left(x+2\right)}:\dfrac{3\left(x+2\right)}{-\left(3-x\right)}\\ =\dfrac{-3\left(x^2+3x+9\right)}{5}\)
\(19,\\ \dfrac{4x^2}{25y^2}:\dfrac{6x}{5y}:\dfrac{2x}{9y}\left(x,y\ne0\right)=\dfrac{4x^2\cdot5y\cdot9y}{25y^2\cdot6x\cdot2x}=\dfrac{3}{5}\)

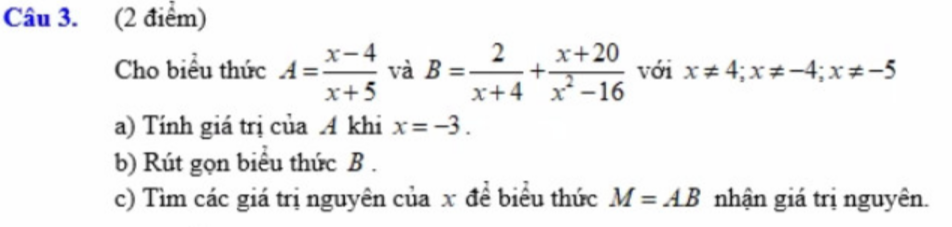


 Mọi người ơi giúp em với ạ, em đang cần gấp, thanks mn
Mọi người ơi giúp em với ạ, em đang cần gấp, thanks mn

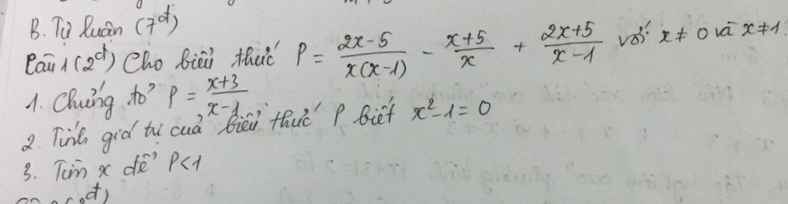 mọi người giúp em với ạ , em đang cần gấp :))
mọi người giúp em với ạ , em đang cần gấp :))
\(a,A=\dfrac{-3-4}{-3+5}=-\dfrac{7}{2}\\ b,B=\dfrac{2x-8+x+20}{\left(x+4\right)\left(x-4\right)}=\dfrac{3\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{3}{x-4}\\ c,M=AB=\dfrac{x-4}{x+5}\cdot\dfrac{3}{x-4}=\dfrac{3}{x+5}\in Z\\ \Leftrightarrow x+5\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-8;-6;-2\right\}\left(x\ne-4\right)\)