Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

Em nên tách ra mỗi bài 1 post thì mọi người sẽ dễ dàng giúp hơn.
Bài 2:
b: Xét ΔADH vuông tại H và ΔAEH vuông tại H có
AH chung
HD=HE
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE

Gọi số đo ba góc A,B,C lần lượt là a, b, c ( kí hiệu độ nhé ), ( a,c,b > 0, a,b,c ∈ N )
Vì ba góc A, B, C tỉ lệ thuận với \(\dfrac{1}{2};\dfrac{1}{3};\dfrac{1}{6}\)nên\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{1}{3}}=\dfrac{c}{\dfrac{1}{6}}\)
Có a + b + c = 180 độ ( tổng ba góc trong một tam giác )
Áp dụng t/c của dãy tỉ số bằng nhau, ta có :
\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{1}{3}}=\dfrac{c}{\dfrac{1}{6}}=\dfrac{\left(a+b+c\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}}=\dfrac{180}{1}=180\)
Có : \(\dfrac{a}{\dfrac{1}{2}}=180=>a=180\cdot\dfrac{1}{2}=90\left(độ\right)\)
\(\dfrac{b}{\dfrac{1}{3}}=180=>b=180\cdot\dfrac{1}{3}=60\left(độ\right)\)
\(\dfrac{c}{\dfrac{1}{6}}=180=>c=180\cdot\dfrac{1}{6}=30\left(độ\right)\)
Vậy, ..


\(C=\dfrac{1}{100}-\left(\dfrac{1}{100\cdot99}+\dfrac{1}{99\cdot98}+...+\dfrac{1}{3\cdot2}+\dfrac{1}{2\cdot1}\right)\\ C=\dfrac{1}{100}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\\ C=\dfrac{1}{100}-\left(1-\dfrac{1}{100}\right)=\dfrac{1}{100}-\dfrac{99}{100}=-\dfrac{98}{100}=-\dfrac{49}{50}\)

a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE và AC=BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I.M,K thẳng hàng


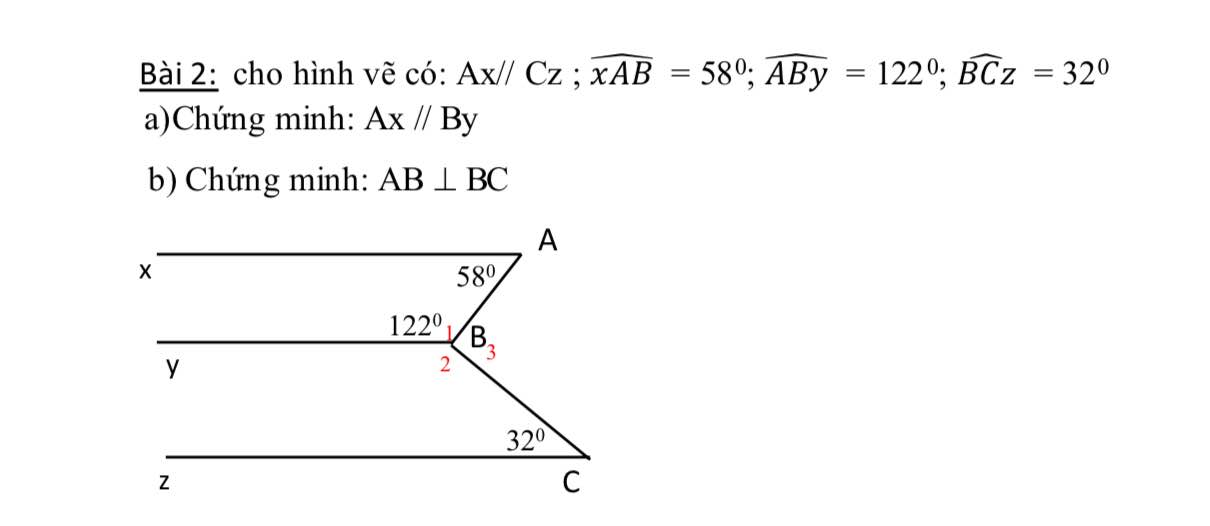
\(a,\widehat{xAB}+\widehat{ABy}=122^0+58^0=180^0\) mà 2 góc này ở vị trí TCP nên Ax//By
\(b,\) Kẻ By' đối By
Ta có Ax//By, Ax//Cz nên By//Cz
Do đó \(\widehat{B_2}+\widehat{BCz}=180^0\left(TCP\right)\Rightarrow\widehat{B_2}=148^0\)
Ta có \(\widehat{B_1}+\widehat{B_2}+\widehat{B_3}=360^0\Rightarrow\widehat{B_3}-360^0-122^0-148^0=90^0\)
Do đó AB vuông góc BC
a) Ta có: \(\widehat{xAB}+\widehat{ABy}=58^0+122^0=180^0\)
Mà 2 góc này trong cùng phía
=> Ax//By
b) Ta có: Ax//By, Ax//Cz
=> By//Cz
\(\Rightarrow\widehat{B_2}=180^0-\widehat{C}=180^0-32^0=148^0\)(trong cùng phía)
\(\Rightarrow\widehat{ABC}=360^0-\widehat{B_1}-\widehat{B_2}=360^0-122^0-148^0=90^0\)
=> AB⊥BC
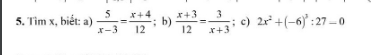

 Mọi người giúp em với ạ
Mọi người giúp em với ạ