
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



18C
22D
26B
Giải thích thêm:
ta có: v=s'(t)=3t²-6t+6
a=s"(t)=6t-6
Thời điểm gia tốc bị triệt tiêu khi a=0
⇔6t-6=0
⇔t=1
Vậy v=3.1²-6.1+6=3 (m/s)
32A
34C
35A
cho mình hỏi là tại sao ở câu 26 lại phải đạo hàm thêm lần nữa vậy?

k ở đây được hiểu là "một số nguyên bất kì", giống hay khác nhau đều được
Ví dụ:
\(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Thì "k" trong \(\dfrac{\pi}{6}+k2\pi\) và "k" trong \(\dfrac{5\pi}{6}+k2\pi\) không liên quan gì đến nhau (nó chỉ là 1 kí hiệu, có thể k trên bằng 0, k dưới bằng 100 cũng được, không ảnh hưởng gì, cũng có thể 2 cái bằng nhau cũng được).
Khi người ta ghi 2 nghiệm đều là "k2pi" chủ yếu do... lười biếng (kiểu như mình). Trên thực tế, rất nhiều tài liệu cũ họ ghi các kí tự khác nhau, ví dụ 1 nghiệm là \(\dfrac{\pi}{6}+k2\pi\), 1 nghiệm là \(\dfrac{5\pi}{6}+n2\pi\) để tránh học sinh phát sinh hiểu nhầm đáng tiếc rằng "2 cái k phải giống hệt nhau về giá trị".

1/
PT $\Leftrightarrow \sin ^2x-(1-\sin ^2x)+\sin x-2=0$
$\Leftrightarrow 2\sin ^2x+\sin x-3=0$
$\Leftrightarrow (\sin x-1)(2\sin x+3)=0$
$\Leftrightarrow \sin x=1$ (chọn) hoặc $\sin x=-\frac{3}{2}< -1$ (loại)
Vậy $\sin x=1$
$\Leftrightarrow x=\frac{\pi}{2}+2k\pi$ với $k$ nguyên.
4/
ĐKXĐ: $\tan x\neq -1$
PT $\Rightarrow \cos ^2x(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin ^2x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin x)(1+\sin x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (\sin x+1)[(1-\sin x)(\cos x-1)-2(\sin x+\cos x)]=0$
$\Leftrightarrow (\sin x+1)(-1-\sin x\cos x-\sin x-\cos x)=0$
$\Leftrightarrow (\sin x+1)^2(\cos x+1)=0$
Nếu $\sin x=-1\Rightarrow x=\frac{-\pi}{2}+2k\pi$ với $k$ nguyên (tm)
Nếu $\cos x=-1\Rightarrow x=\pi +2k\pi$ với $k$ nguyên.







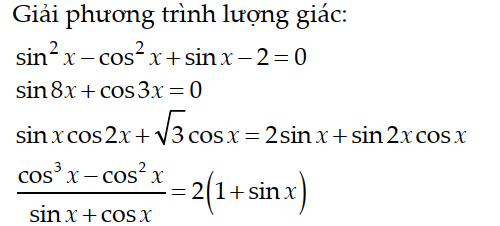

Cái chữ nhìn muốn lé mắt :v
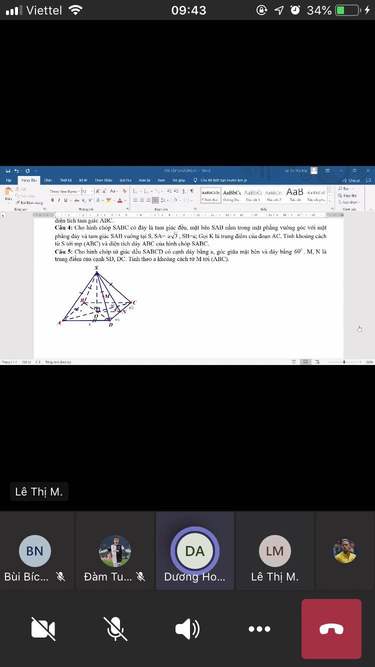
4/ Để tìm \(d\left(S,\left(ABC\right)\right)\) , ta phải hạ được đường vuông góc từ S xuống mp ABC. Nhận thấy \(\left(SAB\right)\perp\left(ABC\right)\) nên ta sẽ nghĩ ngay đến việc hạ đường vuông góc từ S xuống AB. Bởi dựa vô định lý sau: Khi 2 mp vuông góc thì mọi đường thẳng thuộc mp này và vuông góc với giao tuyến 2 mp thì nó sẽ vuông góc với mp còn lại.
Nên từ S ta kẻ \(SH\perp AB;SH\cap AB=\left\{H\right\}\Rightarrow SH\perp\left(ABC\right)\)
\(\Rightarrow SH=d\left(S,\left(ABC\right)\right)\)
\(SH=\dfrac{AS.SB}{\sqrt{AS^2+SB^2}}=....\)
5/ tìm khoảng cách từ M đến mp ABC, nghĩa là tÌm khoảng cách từ M đến mp ABCD
\(SM\cap\left(ABCD\right)=\left\{D\right\}\Rightarrow\dfrac{d\left(S,\left(ABCD\right)\right)}{d\left(M,\left(ABCD\right)\right)}=\dfrac{DS}{DM}=2\)
Vì chóp SABCD đều nên SO sẽ chính là đường cao của chóp
\(\Rightarrow d\left(S,\left(ABCD\right)\right)=SO\)
\(\left(\left(SCD\right),\left(ABCD\right)\right)=\widehat{SNO}=60^0\Rightarrow SO=ON.\tan60^0=\dfrac{a}{2}.\sqrt{3}=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(M,\left(ABCD\right)\right)=\dfrac{a\sqrt{3}}{2.2}=\dfrac{a\sqrt{3}}{4}\)