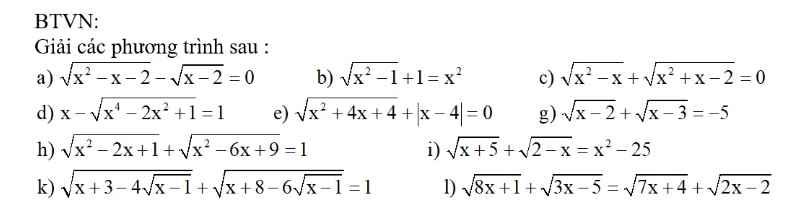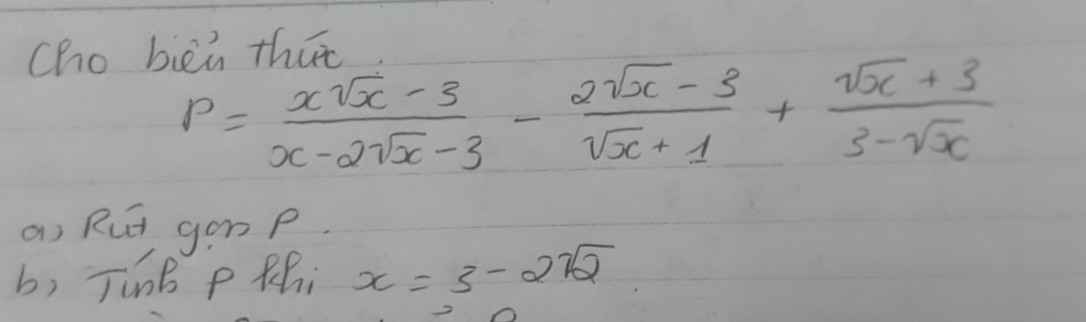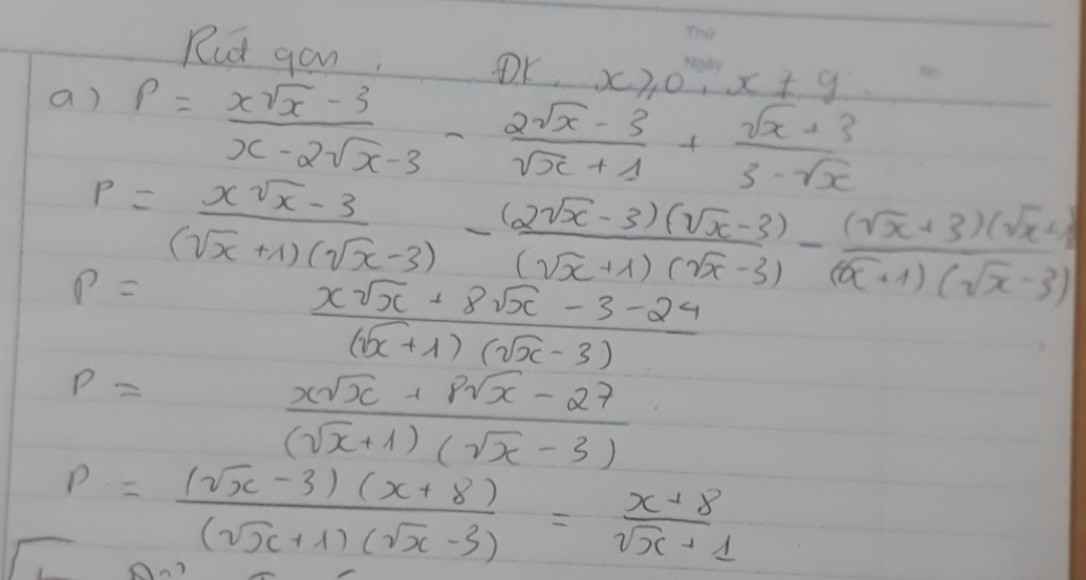K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
2
18 tháng 10 2021
Bài III:
1: Ta có: \(\sqrt{x-3}=5\)
\(\Leftrightarrow x-3=25\)
hay x=28
2: Ta có: \(\dfrac{\sqrt{x}-2}{\sqrt{x}-5}=\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}-6=\sqrt{x}-5\)
\(\Leftrightarrow2\sqrt{x}=1\)
hay \(x=\dfrac{1}{4}\)
6 tháng 9 2021
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
hay \(\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
TH
1
8 tháng 2 2022
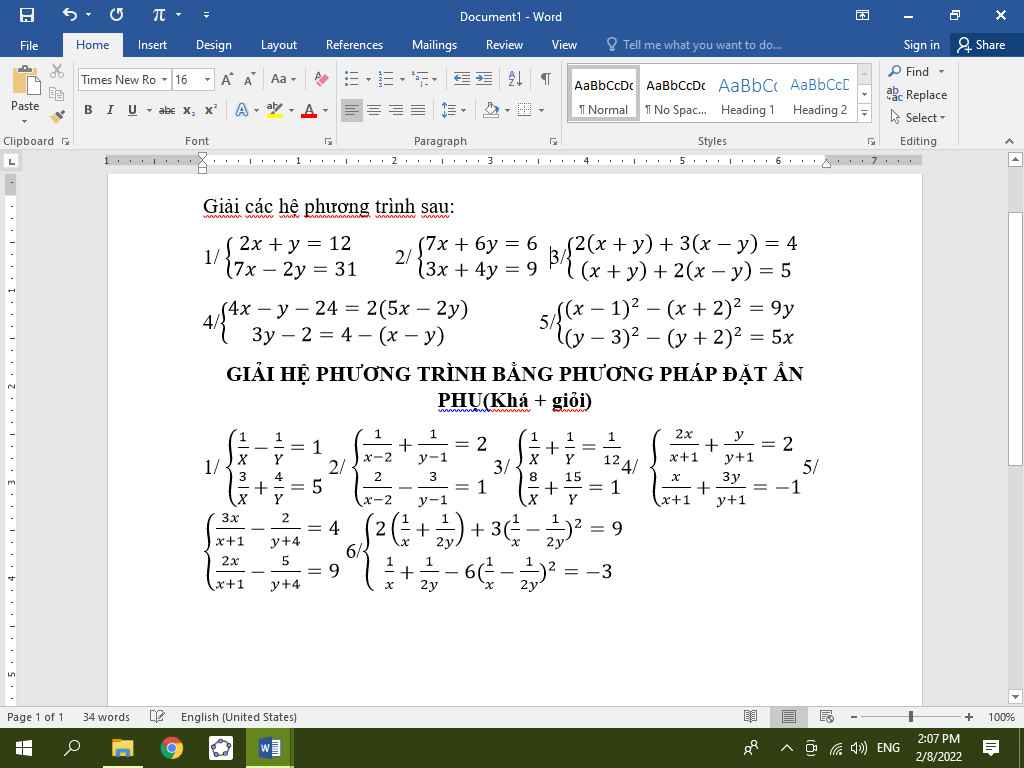
1, \(\left\{{}\begin{matrix}4x+2y=24\\7x-2y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=55\\y=12-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)
2, thiếu đề
4, \(\left\{{}\begin{matrix}4x-y-24=10x-4y\\3y-2=4-x+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\-6x-12y=-36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15y=60\\x=6-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-2\end{matrix}\right.\)
18 tháng 12 2021
a: Xét tứ giác EOBM có
\(\widehat{OBM}+\widehat{OEM}=180^0\)
Do đó: EOBM là tứ giác nội tiếp
NL
3
20 tháng 10 2021
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)
\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
20 tháng 10 2021
\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)
29 tháng 8 2021
thay \(x=3-2\sqrt{2}\) vào P ta có:
\(\dfrac{x+8}{\sqrt{x}+1}=\dfrac{3-2\sqrt{2}+8}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}-1+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}\)
29 tháng 8 2021
\(b,x=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^2\)
Thay vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+8}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}=\dfrac{11\sqrt{2}-4}{2}\)
TH
0
1 tháng 7 2023
8.31:
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
XétΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
=>MN vuông góc MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc NMQ=90 độ
=>MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn
