
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
c) Ta có: \(x^4+3x^2-4=0\)
\(\Leftrightarrow x^4+4x^2-x^2-4=0\)
\(\Leftrightarrow\left(x^2+4\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow x^2=1\)
hay \(x\in\left\{1;-1\right\}\)
Bài 5:
b) Ta có: \(\dfrac{x+1}{99}+\dfrac{x+2}{98}=\dfrac{x+3}{97}+\dfrac{x+4}{96}\)
\(\Leftrightarrow\dfrac{x+100}{99}+\dfrac{x+100}{98}-\dfrac{x+100}{97}-\dfrac{x+100}{96}=0\)
\(\Leftrightarrow x+100=0\)
hay x=-100

\(P=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\) (Đk:\(a>0\))
\(=\dfrac{\sqrt{a}\left(a\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)
\(=\sqrt{a}\left(\sqrt{a}+1\right)-2\sqrt{a}-1+1\)
\(=a-\sqrt{a}\)
b) \(P=2\Leftrightarrow a-\sqrt{a}=2\Leftrightarrow a-\sqrt{a}-2=0\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{a}=2\\\sqrt{a}=-1\left(vn\right)\end{matrix}\right.\)\(\Rightarrow a=4\) (tm)
Vậy a=4 thì P=2
c) \(P=a-\sqrt{a}=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu "=" xảy ra khi \(\sqrt{a}=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{4}\)
Vậy \(P_{min}=-\dfrac{1}{4}\)
Coi pt \(a-\sqrt{a}-2=0\) là pt ẩn \(\sqrt{a}\)
Hoặc e đặt \(t=\sqrt{a}\)
Pt tt: \(t^2-t-2=0\) \(\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{a}=-1\\\sqrt{a}=2\end{matrix}\right.\)

8.31:
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
XétΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
=>MN vuông góc MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc NMQ=90 độ
=>MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn

bài 2
a, \(3\sqrt{8}\) + \(\sqrt{18}\) - \(\sqrt{72}\)
=\(6\sqrt{2}\)+\(3\sqrt{2}\)-\(6\sqrt{2}\)
=\(3\sqrt{2}\)(3+1-3)
=3\(\sqrt{2}\)

câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)

ĐKXĐ: \(x\le3\)
\(P=\sqrt{3-x}-\left(3-x\right)+3=-\left(\sqrt{3-x}-\dfrac{1}{2}\right)^2+\dfrac{13}{4}\le\dfrac{13}{4}\)
\(P_{max}=\dfrac{13}{4}\) khi \(\sqrt{3-x}=\dfrac{1}{2}\Leftrightarrow x=\dfrac{11}{4}\)



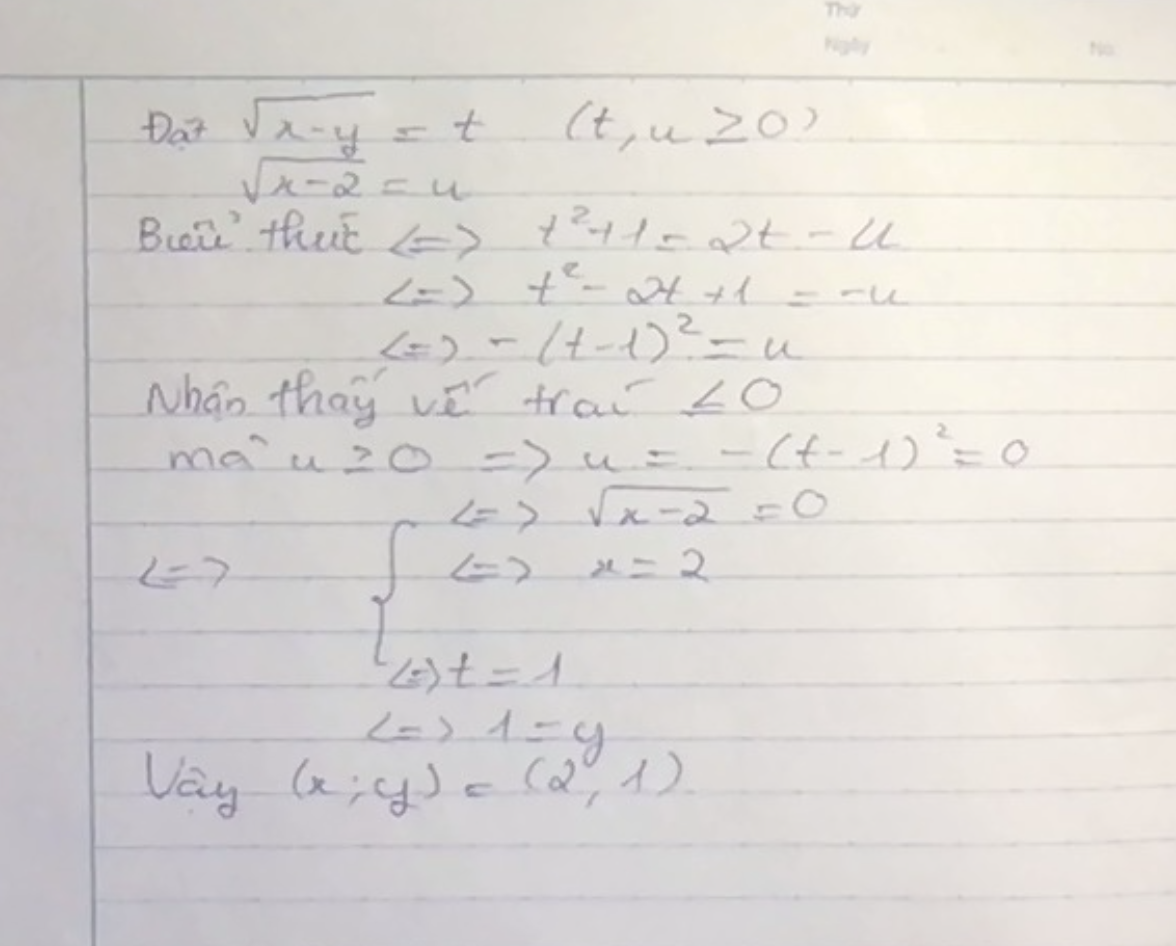




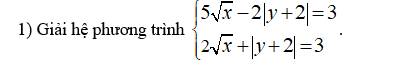

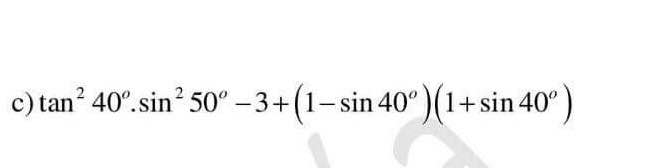 mọi người giải giúp em câu này vs ạ
mọi người giải giúp em câu này vs ạ
9.
a, \(x^4-x^3-14x^2+x+1=0\)
\(< =>x^4+3x^3-x^2-4x^3-12x^2+4x-x^2-3x+1=0\)
\(< =>x^2\left(x^2+3x-1\right)-4x\left(x^2+3x-1\right)-\left(x^2+3x-1\right)=0\)
\(< =>\left(x^2-4x-1\right)\left(x^2+3x-1\right)=0\)
\(=>\left[{}\begin{matrix}x^2-4x-1=0\left(1\right)\\x^2+3x-1=0\left(2\right)\end{matrix}\right.\)
giải pt(1) \(=>x^2-4x+4-5=0< =>\left(x-2\right)^2-\sqrt{5}^2=0\)
\(=>\left(x-2-\sqrt{5}\right)\left(x-2+\sqrt{5}\right)=0\)
\(=>\left[{}\begin{matrix}x=2+\sqrt{5}\\x=2-\sqrt{5}\end{matrix}\right.\)
giải pt(2) \(\)\(=>x^2+3x-1=0< =>x^2+2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{13}{4}=0\)
\(< =>\left(x+\dfrac{3}{2}\right)^2-\left(\dfrac{\sqrt{13}}{2}\right)^2=0\)
\(=>\left(x+\dfrac{3}{2}+\dfrac{\sqrt{13}}{2}\right)\left(x+\dfrac{3}{2}-\dfrac{\sqrt{13}}{2}\right)=0\)
tương tự cái pt(1) ra nghiệm rồi kết luận
b, đặt \(\sqrt{x^2+1}=a\left(a\ge1\right)=>x^2+1=a^2\)
\(=>x^4=\left(a^2-1\right)^2\)
\(=>pt\) \(\left(a^2-1\right)^2+a^2.a-1=0\)
\(=>a^4-2a^2+1+a^3-1=0\)
\(< =>a^4-2a^2+a^3=0< =>a^2\left(a+2\right)\left(a-1\right)=0\)
\(->\left[{}\begin{matrix}a=0\left(ktm\right)\\a=-2\left(ktm\right)\\a=1\left(tm\right)\end{matrix}\right.\)rồi thế a vào \(\sqrt{x^2+1}\)
\(=>x=0\)