Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng. Vì √0,0001=√0,012=0,010,0001=0,012=0,01
Vì VP=√0,0001=√0,012=0,01=VTVP=0,0001=0,012=0,01=VT.
b) Sai.
Vì vế phải không có nghĩa do số âm không có căn bậc hai.
c) Đúng.
Vì: 36<39<4936<39<49 ⇔√36<√39<√49⇔36<39<49
⇔√62<√39<√72⇔62<39<72
⇔6<√39<7⇔6<39<7
Hay √39>639>6 và √39<739<7.
d) Đúng.
Xét bất phương trình đề cho:
(4−√13).2x<√3.(4−√13)(4−13).2x<3.(4−13) (1)(1)
Ta có:
16>13⇔√16>√1316>13⇔16>13
⇔√42>√13⇔42>13
⇔4>√13⇔4>13
⇔4−√13>0⇔4−13>0
Chia cả hai vế của bất đẳng thức (1)(1) cho số dương (4−√13)(4−13), ta được:
(4−√13).2x(4−√13)<√3.(4−√13)(4−√13)(4−13).2x(4−13)<3.(4−13)(4−13)
⇔2x<√3.⇔2x<3.
Vậy phép biến đổi tương đương trong câu d là đúng.

a) Đúng, v ì √ 0 , 0001 = √ 0 , 01 2 = 0 , 01
b) Sai, vì vế phải không có nghĩa.
(Lưu ý: √A có nghĩa khi A ≥ 0)
c) Đúng, v ì 7 = √ 7 2 = √ 49 > √ 39
6 = √ 6 2 = √ 36 < √ 39
d) Đúng, v ì 4 - √ 13 = √ 4 2 - √ 13 = √ 16 - √ 13 > 0
Do đó: (4 - √13).2x < √3(4 - √13) (giản ước hai vế với (4 - √13))
⇔ 2x < √3

a) Ta có: \(\left(\sqrt{7}-\sqrt{2}\right)\cdot\sqrt{9+2\sqrt{14}}\)
\(=\left(\sqrt{7}-\sqrt{2}\right)\cdot\left(\sqrt{7}+\sqrt{2}\right)\)
=7-2
=5
d) Ta có: \(\dfrac{1}{\sqrt{8}+\sqrt{7}}+\sqrt{175}-\dfrac{6\sqrt{2}-4}{3-\sqrt{2}}\)
\(=2\sqrt{2}-\sqrt{7}+5\sqrt{7}-\dfrac{2\sqrt{2}\left(3-\sqrt{2}\right)}{3-\sqrt{2}}\)
\(=2\sqrt{2}+4\sqrt{7}-2\sqrt{2}\)
\(=4\sqrt{7}\)

a/ \(=\sqrt{\left(\sqrt{3}-1\right)^2\left(2\sqrt{3}+1\right)^2}\)
\(=\left(\sqrt{3}-1\right)\left(2\sqrt{3}+1\right)=5-\sqrt{3}\)
b/ \(=\left(\sqrt{3}-2\right)\left(\sqrt{3}+1\right)\sqrt{4+2\sqrt{3}}\)
\(=\left(\sqrt{3}-2\right)\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=\left(\sqrt{3}-2\right)\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right)=\left(\sqrt{3}-2\right)\left(\sqrt{3}+1\right)^2\)
\(=\left(\sqrt{3}-2\right)\left(4+2\sqrt{3}\right)=2\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)\)
\(=2\left(3-4\right)=-2\)
c/ \(=\left(3+\sqrt{5}\right)\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\)
\(=\left(3+\sqrt{5}\right)\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=\left(3+\sqrt{5}\right)\left(\sqrt{5}-1\right)^2=\left(3+\sqrt{5}\right)\left(6-2\sqrt{5}\right)\)
\(=2\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)=2.\left(9-5\right)=8\)
d/ \(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=2\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)=2\left(16-15\right)=2\)

a) \(\sqrt{25}+\sqrt{9}-\sqrt{16}\) = \(\sqrt{5^2}+\sqrt{3^2}-\sqrt{4^2}\) = 5 + 3 - 4 = 4
b) \(\sqrt{0,16}+\sqrt{0,01}+\sqrt{0,25}\) = 0,4 + 0,1 + 0,5 = 1
c) \(\left(\sqrt{3^2}\right)-\left(\sqrt{2^2}\right)+\left(\sqrt{5^2}\right)\)
= 3 - 2 + 5 = 6
d) \(\sqrt{4}-\left(-\sqrt{3}\right)^2+\sqrt{49}\) = 2 - 3 + 7 = 6
e) \(\left(2\sqrt{2}\right)^2-\left(3\sqrt{3}\right)^2\)
= \(\left(\sqrt{8}\right)^2-\left(\sqrt{27}\right)^2\) = 8 - 27 = -19
f) \(\left(-2\sqrt{2}\right)^2+\left(3\sqrt{3}\right)^2\) = 8 + 27 = 35

\(a.\left(2-\sqrt{3}\right)\sqrt{7+4\sqrt{3}}=\left(2-\sqrt{3}\right)\sqrt{4+2.2\sqrt{3}+3}=\left(2-\sqrt{3}\right)\sqrt{\left(2+\sqrt{3}\right)^3}\) = \(\left(2-\sqrt{3}\right)\) | \(2+\sqrt{3}\) | = \(4-3=1\)
\(b.\sqrt{13+4\sqrt{10}}+\sqrt{13-4\sqrt{10}}=\sqrt{8+2.2\sqrt{2}.\sqrt{5}+5}+\sqrt{8-2.2\sqrt{2}.\sqrt{5}+5}=\sqrt{\left(2\sqrt{2}+\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}\) \(=\) | \(2\sqrt{2}+\sqrt{5}\) | \(+\) | \(2\sqrt{2}-\sqrt{5}\) | \(=4\sqrt{2}+2\sqrt{5}\)
\(c.\sqrt{7-3\sqrt{5}}=\dfrac{\sqrt{14-2.3\sqrt{5}}}{\sqrt{2}}=\dfrac{\sqrt{9-2.3\sqrt{5}+5}}{\sqrt{2}}=\dfrac{\sqrt{\left(3-\sqrt{5}\right)^2}}{\sqrt{2}}\)\(=\) \(\dfrac{\text{ |}3-\sqrt{5}\text{ |}}{\sqrt{2}}\) \(=\dfrac{3-\sqrt{5}}{\sqrt{2}}\)
\(d.\) Tương Tự nhé bạn.
a) Đúng
b) Sai. Số âm không có căn bậc hai.
c) Đúng vì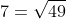 và
và 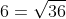 .
.
d) Đúng vì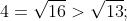 do đó
do đó