K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 5 2022
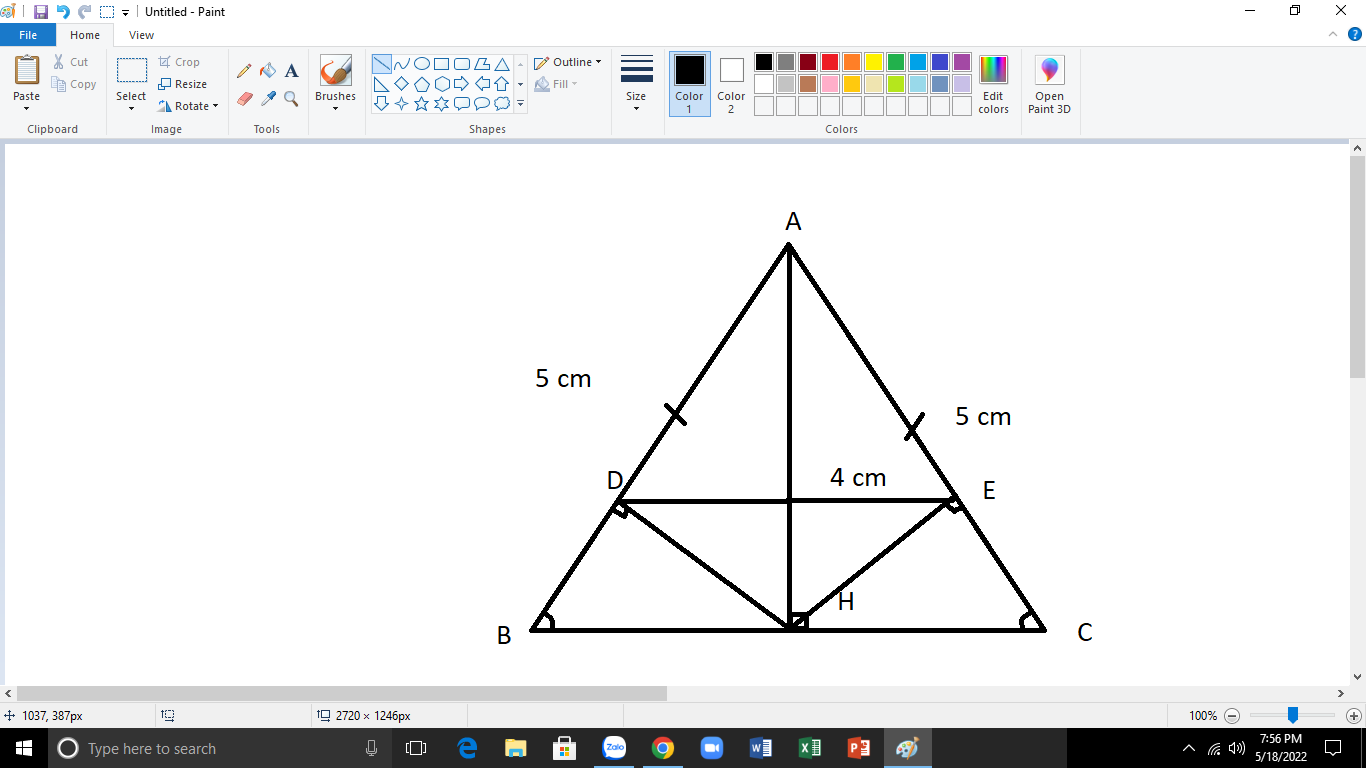
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH và \(\widehat{BAH}=\widehat{CAH}\)
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
d: XétΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tạiA
19 tháng 5 2022
\(\text{a)Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(\left\{{}\begin{matrix}AH\text{ chung}\\AB=AC=5cm\left(gt\right)\\\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c-g-c\right)\)
\(\Rightarrow BH=CH\left(\text{hai cạnh tương ứng}\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Xét }\Delta BAH\text{ vuông tại H có:}\)
\(AB^2=AH^2+BH^2\left(\text{định lí Py ta go}\right)\)
\(\Rightarrow BH^2=AB^2-AH^2\)
\(\Rightarrow BH^2=5^2-4^2=25-16=9\left(cm\right)\)
\(\Rightarrow BH=\sqrt{9}=3\left(cm\right)\)
\(\text{d)Xét }\Delta ADH\text{ và }\Delta AEH\text{ có:}\)
\(\left\{{}\begin{matrix}AH\text{ chung}\\\widehat{ADH}=\widehat{AEH}=90^0\left(gt\right)\\\widehat{DAH}=\widehat{EAH}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADH=\Delta AEH\left(g-c-g\right)\)
\(\Rightarrow AD=AE\left(\text{hai cạnh tương ứng}\right)\)
\(\Rightarrow\Delta ADE\text{ cân tại A}\)
18 tháng 5 2022
a,
Ta có :
2BD = BC
=> 2BD = 6
=> BD = 3 (cm)
Ta có :
Δ ABC cân tại A
AD là đường trung trực
=> AD là đường cao
=> AD là đường trung tuyến
Xét Δ ADB vuông tại D, có :
\(AB^2=AD^2+BD^2\) (Py - ta - go)
=> \(6^2=AD^2+3^2\)
=> \(27=AD^2\)
=> AD = 5,1 (cm)
18 tháng 5 2022
b,
Xét Δ ABG và Δ ACG, có :
AG là cạnh chung
AB = AC (Δ ABC cân tại A)
\(\widehat{BAG}=\widehat{CAG}\) (AD là tia phân giác \(\widehat{BAC}\))
=> Δ ABG = Δ ACG (c.g.c)
=> \(\widehat{ABG}=\widehat{ACG}\)
c,
Ta có :
G là trọng tâm
Mà AD là đường trung trực
=> A,G,D thẳng hàng
d,
Điều cần chứng minh : BC + 2AD > AB + AC
Ta có :
BC = 6 (cm)
AD = 5,1 (cm)
AB = AC = 5 (cm)
Thế số :
6 + 2. 5,1 > 5 + 5
=> 16,2 > 10
=> BC + 2AD > AB + AC (đpcm)
TA
1
10 tháng 5 2022
a, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=10^2+8^2\)
=> \(BC^2=164\)
=> \(BC=12,8\left(cm\right)\)
b, Xét Δ ABE và Δ HBE, có :
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác \(\widehat{ABC}\))
\(\widehat{BAE}=\widehat{BHE}=90^o\)
BE là cạnh chung
=> Δ ABE = Δ HBE (g.c.g)
=> AB = HB
Xét Δ ABH, có : AB = HB (cmt)
=> Δ ABH cân tại B
c,
Gọi O là giao điểm của tia AH và BE
Xét Δ cân ABH, có :
BO là tia phân giác \(\widehat{ABH}\)
=> BO là đường cao
=> \(BO\perp AH\)
=> \(BE\perp AH\)
10 tháng 5 2022
`P(0) = c vdots 3`.
`P(1) = a + b + c vdots 3` mà `c vdots 3 => a + b vdots 3`.
`P(-1) = a - b + c vdots 3` mà `c` vdots 3 => a - b vdots 3`.
`=> a, b vdots 3`.
`=> abc vdots 3 xx 3 xx 3 = 27 => dpcm`.
AD
10 tháng 5 2022
P(x) chia hết cho 3 với mọi giá trị của x
\(\Rightarrow\) \(\left\{{}\begin{matrix}a⋮x\\b⋮x\\c⋮x\end{matrix}\right.\)\(\Rightarrow abc⋮3\cdot3\cdot3\Rightarrow abc⋮27\)
30 tháng 4 2022
Bài 6:
a: Đặt 4x-1/2=0
=>4x=1/2
hay x=1/8
b: Đặt (x-1)(x+1)=0
=>x-1=0 hoặc x+1=0
=>x=1 hoặc x=-1
TA
Mng giúp mình bài 1, 2, 3, 4 nha(vẽ hình luôn). Cảm ơn nhiều 🤩
1
TA
2
10 tháng 5 2022
a: Xét ΔBMA vuông tại M và ΔBMC vuông tại M có
BM chung
BA=BC
Do đó: ΔBMA=ΔBMC
b: Xét ΔBEM vuông tại E và ΔBFM vuông tại F có
BM chung
\(\widehat{EBM}=\widehat{FBM}\)
Do đó: ΔBEM=ΔBFM
Suy ra: BE=BF và ME=MF
=>BM là đường trung trực của EF
c: Xét ΔBAC có BE/BA=BF/BC
nên EF//AC
30 tháng 4 2022
\(=1\cdot\left(-1\right)+\left(-1\right)^2\cdot2^2+1^3\cdot2^3=8-1+4=11\)
Bài 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔBAC vuông tại A
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
SUy ra: BA=BE và DA=DE
hay BD là đường trung trực của AE
c: BF=BA+AF
BC=BE+EC
mà BA=BE
và AF=EC
nên BF=BC
hay ΔBFC cân tại B
Bạn ơi bài 6 giúp mk luôn ạ