NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7N
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
4
6 tháng 1 2020
13+23+33+...+1003
=1+2+1.2.3+3+2.3.4+100+99.100.101
=(1+2+3+...+100)+(1.2.3+2.3.4+...+99.100.101)
=5050+101989800
=101994850
NHỚ T.I.C.K và KB với mk nha
TN
2
19 tháng 12 2021
Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
19 tháng 12 2021
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)
3 tháng 8 2019
Câu 1: (2 điểm) Cho biểu thức:
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số 
sao cho 
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n thuộc N*. Hãy so sánh 
b. Cho 
. So sánh A và B.
Câu 5: (2 điểm)
Cho 10 số tự nhiên bất kỳ: a1, a2, ....., a10. Chứng minh rằng thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.
Câu 6: (1 điểm)
Cho 2006 đường thẳng trong đó bất kì 2 đường thẳng nào cũng cắt nhau. Không có 3 đường thẳng nào đồng qui. Tính số giao điểm của chúng.
Câu 1: (2 điểm) Cho biểu thức:
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số sao cho
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n thuộc N*. Hãy so sánh
b. Cho . So sánh A và B.
Câu 5: (2 điểm)
Cho 10 số tự nhiên bất kỳ: a1, a2, ....., a10. Chứng minh rằng thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.
Câu 6: (1 điểm)
Cho 2006 đường thẳng trong đó bất kì 2 đường thẳng nào cũng cắt nhau. Không có 3 đường thẳng nào đồng qui. Tính số giao điểm của chúng.
T.I.C.K nha
TD
0
giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ
1 tháng 11 2021
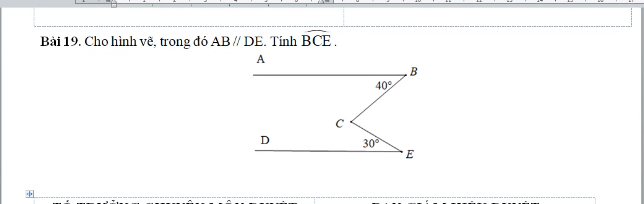
Kẻ CF//AB thì CF//DE
Do đó \(\widehat{BCF}=\widehat{ABC}=40^0;\widehat{FCE}=\widehat{CED}=30^0\) (so le trong)
Vậy \(\widehat{BCE}=\widehat{BCF}+\widehat{FCE}=30^0+40^0=70^0\)
7N
giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
0
N
13 tháng 11 2021
Bài 6:
Gọi số giấy vụn 3 lớp thu được lần lượt là: \(a,b,c\left(a,b,c>0\right)\)
Áp dụng TCDTSBN:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{150}{15}=10\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\cdot10=30\left(kg\right)\\b=5\cdot10=50\left(kg\right)\\c=7\cdot10=70\left(kg\right)\end{matrix}\right.\)
13 tháng 11 2021
Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{-21}{7}=-3\)
Do đó: x=-6; y=-15
