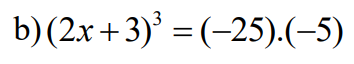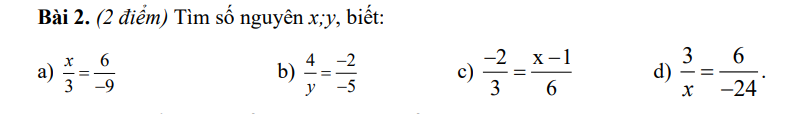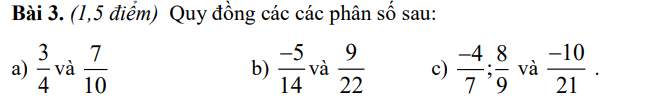Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(2x+3\right)^3=\left(-25\right).\left(-5\right)\)
\(\Leftrightarrow\left(2x+3\right)^3=125\)
\(\Leftrightarrow\left(2x+3\right)^3=5^3\)
\(\Leftrightarrow2x+3=5\)
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)

\(\Leftrightarrow x\left(y+1\right)+y+1=31\\ \Leftrightarrow\left(x+1\right)\left(y+1\right)=31=31\cdot1\)
\(TH_1:\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\rightarrow\left(30;0\right)\\ TH_2:\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\rightarrow\left(0;30\right)\)
Vậy \(\left(x;y\right)\in\left\{\left(30;0\right);\left(0;30\right)\right\}\)
\(\Leftrightarrow xy+x+y+1=31\Leftrightarrow\left(x+1\right)\left(y+1\right)=31\)
Do x, y nguyên dương nên xảy ra các TH sau:
TH1: \(\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\)(LOẠI)
TH2:\(\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\)(LOẠI)
Vậy không có x, y nguyên dương thoả mãn đề bài.


\(a,\dfrac{x}{3}=\dfrac{6}{-9}\\ \Rightarrow x=-\dfrac{2}{3}.3\\ \Rightarrow x=-2\\ b,\dfrac{4}{y}=\dfrac{-2}{-5}\\ \Rightarrow y=4:\dfrac{2}{5}\\ \Rightarrow y=10\\ c,\dfrac{-2}{3}=\dfrac{x-1}{6}\\ \Rightarrow3x-3=-12\\ \Rightarrow3x=-9\\ \Rightarrow x=-3\\ d,\dfrac{3}{x}=\dfrac{6}{-24}\\ \Rightarrow x=3:-\dfrac{1}{4}\\ \Rightarrow x=-12\)

\(a,\dfrac{3}{4}=\dfrac{15}{20}\\ \dfrac{7}{10}=\dfrac{14}{20}\\ b,\dfrac{-5}{14}=\dfrac{-55}{154}\\ \dfrac{9}{22}=\dfrac{63}{154}\\ \dfrac{-4}{7}=\dfrac{-36}{63}\\ \dfrac{8}{9}=\dfrac{56}{63}\\ \dfrac{-10}{21}=\dfrac{-30}{63}\)

a: Để 5/n-1 là số nguyên thì \(n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)
b: Để n+8/n+1 là số nguyên thì \(n+1\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{0;-2;6;-8\right\}\)
Để 5/n-1 nhận giá trị là số nguyên thì:
n+1 thuộc Ư(5)= {-1;1;-5;5}
Lập bảng:
| n+1 | 1 | -1 | -5 | 5 |
| n | 0 | -2 | -6 | 4 |
=> n thuộc {0;-2;-6;4} thì n sẽ nhận giá trị là số nguyên
câu b làm tương tượng nhưng lấy n+1 thuộc Ư(7)

Bài 4:
Gọi số học sinh là x
Theo đề, ta có: \(x\in BC\left(15;18;20\right)\)
hay x=540

2,
\(a,\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{97.99}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\\ =1-\dfrac{1}{99}\\ =\dfrac{98}{99}\)
\(b,\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{40.43}\\ =\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{40.43}\right):3\\ =\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{40}-\dfrac{1}{43}\right):3\\ =\left(1-\dfrac{1}{43}\right):3\\ =\dfrac{42}{43}:3=\dfrac{14}{43}\)

Bài 6 :
a) 7n + 10 và 5n + 7
ƯCLN( 7n + 10 ; 5n + 7 ) = d
=> 7n + 10 chia hết d
5n + 7 chia hết d
5.(7n + 10) = 35n + 50 chia hết d
7.(5n + 7 ) = 35n + 49 chia hết d
=> ( 35n + 50 ) - ( 35n + 49 ) chia hết d
35n + 50 - 35n - 49 chia hết d
( 35n - 35n ) + ( 50 - 49 ) chia hết d
0 + 1 chia hết d
=> 1 chia hết d
suy ra d = 1
Vậy ƯCLN ( 7n + 10 ; 5n + 7 ) = 1
b) làm tương tự câu a
Bài 7 :
a) Chứng minh chia hết 4
A = 31 + 32 + 33 +... + 3119 + 3120
A = ( 31 + 32 ) + (33 + 34 ) + ... + ( 3119 + 3120 )
A = 31 . ( 1 + 3 ) + 33 . ( 1 + 3 ) + ... + 3119. ( 1 + 3 )
A = 31 . 4 + 33 . 4 + ... + 3119 . 4
A = 4. ( 31 + 33 + ... + 3119 ) chia hết 4
Chia hết cho 13 thì làm tương tự
Câu b mik chx bt làm ^.^