K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PQ
0
13 tháng 6 2023
3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM
MH
25 tháng 9 2021
1) \(\sqrt{2x-5}=7\)
\(\left(\sqrt{2x-5}\right)^2=7^2\)
\(2x-5=49\)
\(2x=54\)
\(x=27\)
2) \(3+\sqrt{x-2}=4\)
\(\sqrt{x-2}=1\)
\(\left(\sqrt{x-2}\right)^2=1^2\)
\(x-2=1\)
\(x=3\)
25 tháng 9 2021
1) \(\sqrt{2x-5}=7\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow2x-5=49\Leftrightarrow2x=54\Leftrightarrow x=27\left(tm\right)\)
2) \(3+\sqrt{x-2}=4\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
3) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}=1\Leftrightarrow\left|x-1\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4) \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\Leftrightarrow\left|x-2\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5) \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+4\right)^2}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+4\\2x-1=-x-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
6) \(ĐK:x\ge-2\)
\(\Leftrightarrow5\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow x+2=x+7\Leftrightarrow2=7\left(VLý\right)\)
Vậy \(S=\varnothing\)
7) \(ĐK:x\ge-1\)
\(\Leftrightarrow5\sqrt{2x+1}+3\sqrt{x+1}=4\sqrt{x+1}+4\sqrt{2x+1}\)
\(\Leftrightarrow\sqrt{2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow2x+1=x+1\Leftrightarrow x=0\left(tm\right)\)
29 tháng 10 2021
2: Để (d)//y=(m2+1)x-4 thì \(\left\{{}\begin{matrix}m^2=1\\m-5\ne-4\end{matrix}\right.\Leftrightarrow m=1\)
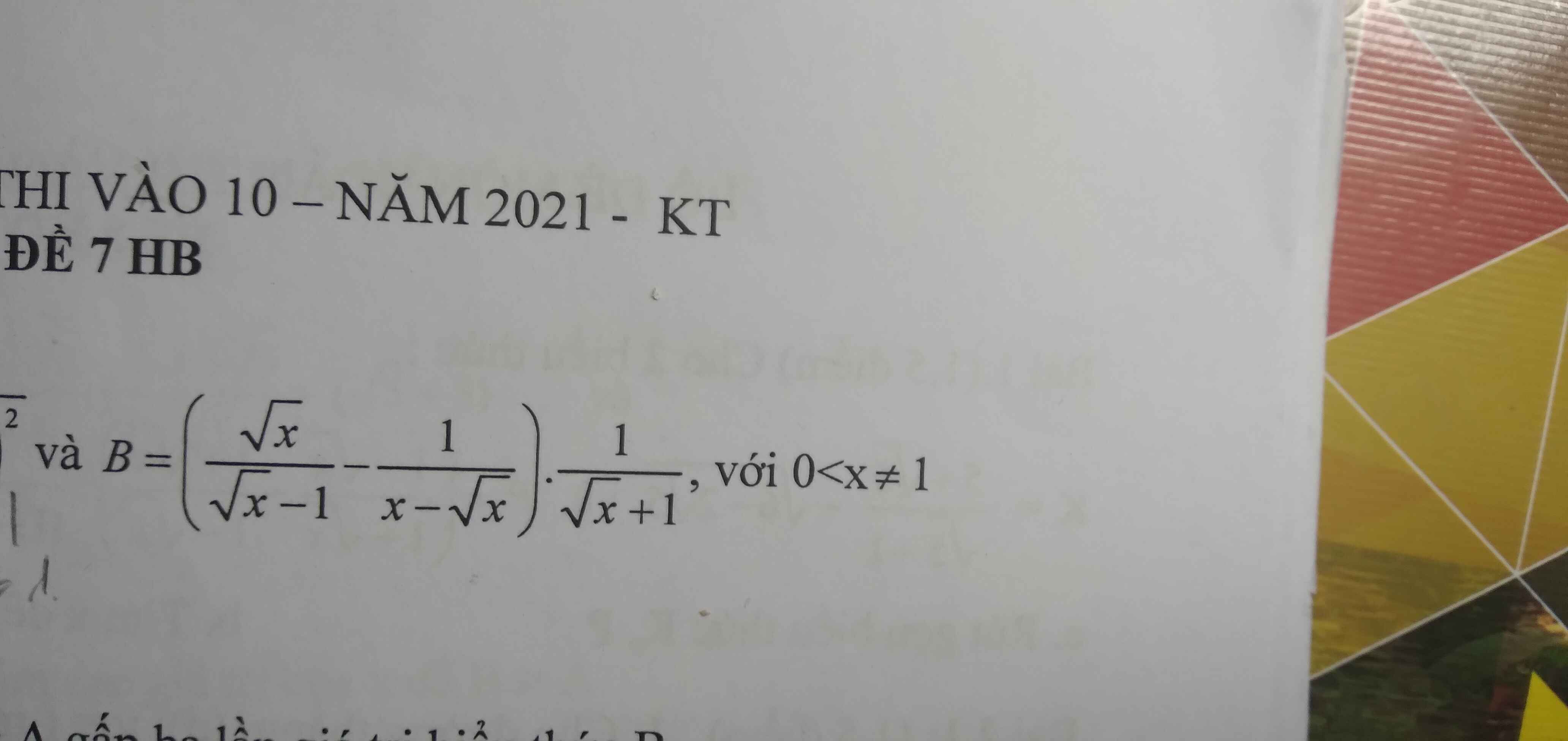
\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right).\dfrac{1}{\sqrt{x}+1}\)
\(\Rightarrow B=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\dfrac{1}{\sqrt{x}+1}\)
\(\Rightarrow B=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{1}{\sqrt{x}+1}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow B=\dfrac{1}{\sqrt{x}}\)
Bạn cần làm j với B