BG
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HK
1
DC
2 tháng 3 2022
khuyến cáo ko nên gạt xuống.
Đồ ngu đồ ăn hại cút mịa mài đê :D
4 tháng 12 2021
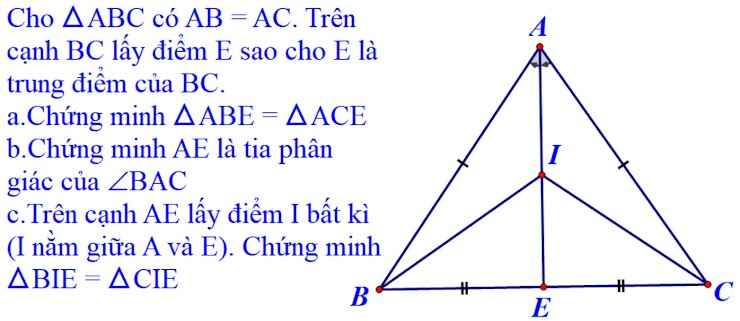
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
KN
11 tháng 9 2019
\(\left(x+2\right)\left(x-3\right)\left(x-6\right)< 0\)
Suy ra phải có ít nhất 1 số âm
Lại có: \(x-6< x-3< x+2\)
nên \(\hept{\begin{cases}x-6< 0\\x-3>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 6\\x>3\end{cases}}\Leftrightarrow3< x< 6\)
TL
19 tháng 10 2019
a, |x-2|+x
TH1: |x-2|=x-2
=> |x-2|+x=x-2+x=2x-2
TH2: |x-2|=-(x-2)= -x+2
=> |x-2|+x= -x+2+x=2
29 tháng 10 2021
Bài 5:
\(A=2A-A=2^2+2^3+...+2^{107}-2-2^2-...-2^{2016}=2^{107}-2\)
\(2\left(A+2\right)=2^{2x}\\ \Rightarrow2\left(2^{107}-2+2\right)=2^{2x}\\ \Rightarrow2^{108}=2^{2x}\\ \Rightarrow2x=108\\ \Rightarrow x=54\)
29 tháng 10 2021
Bài 3:
Gọi số học sinh lớp 7A, 7B lần lượt là a,b
Ta có: \(\left\{{}\begin{matrix}\dfrac{x}{8}=\dfrac{y}{9}\\y-x=5\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-1}=\dfrac{5}{1}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{9}=5\Rightarrow y=45\)
Vậy số học sinh lớp 7A, 7B lần lượt là 40, 45 học sinh
AM
2
BD
20 tháng 8 2017
2x = 8y + 1
2x luôn có chữ số tận cùng là 2 ; 4 ; 8 ; 6
8y + 1 = 2x nên 8y phải có chữ số tận cùng là 1 ; 3 ; 7 ; 5
Nhưng 8y chỉ có thể có tận cùng là 8 ; 4 ; 2 ; 6
Vậy không tồn tại bất kì giá trị x;y nào thỏa mãn .
\(\left(x+2021\right)\left(\dfrac{1}{2}-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-2021\\x=\dfrac{1}{2}\end{matrix}\right.\)