
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì \(RN=NQ,QM=QP\Rightarrow MN\) là đường trung bình tam giác PQR
\(\Rightarrow PQ=2MN=2.22,125=44,25\)


<=> (x+2 ) (x2 - 3x + 5 ) - (x+2 ) x2=0
<=> (x+ 2 ) (x2-3x + 5 - x2) =0
<=> (x + 2 ) (-3x+5)=0
<=> x+2 = 0 hoặc -3x+5=0
x = -2 -3x = -5
x=5/3

Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\\
\Rightarrow\dfrac{2}{4}=\dfrac{3}{x}\\
\Rightarrow x=3:\dfrac{1}{2}\\
\Rightarrow x=6\left(cm\right)\)


a: \(2x^2\left(3xy+x^2-2y^2\right)\)
\(=6x^3y+2x^4-4x^2y^2\)
b: \(\dfrac{1}{3}x^2y^3\left(2x-3y+1\right)\)
\(=\dfrac{2}{3}x^3y^3-x^2y^4+\dfrac{1}{3}x^2y^3\)
h: \(\left(x-1\right)\left(x+1\right)\left(2x-3\right)\)
\(=\left(x^2-1\right)\left(2x-3\right)\)
\(=2x^3-3x^2-2x+3\)

Bài 1:
\(a,=x^2-4-x^2-4x-4=-4x-8\\ b,=x^2-4-x^2+2x+3=2x-1\\ c,=x^2-4-x^2-3x+10=-3x+6\\ d,=\left(6x+1-6x+1\right)^2=4\\ e,=25y^2-9-25y^2+40y-16=40y-25\\ f,=\left(2x+1+2x-1\right)^2=16x^2\\ g,=\left(x-3\right)\left(x+3-x+3\right)=9\left(x-3\right)=9x-27\\ h,=\left(x^2-2x+1\right)\left(x+2\right)-x^3+8\\ =x^3-3x+2-x^3+8=-3x+10\\ i,=4x^2-12x-6x-3x^2=x^2-18x\\ k,=10x^2+4x+6x^2-11x+3=16x^2-7x+3\)



 help em vs mn ơi
help em vs mn ơi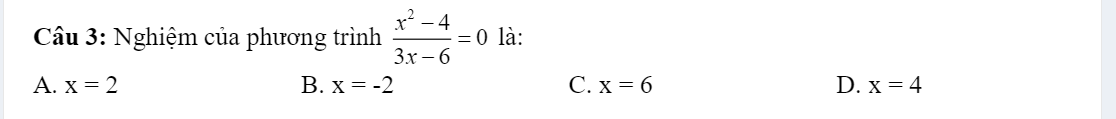
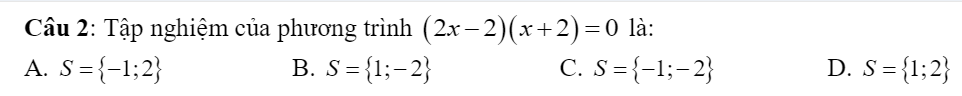
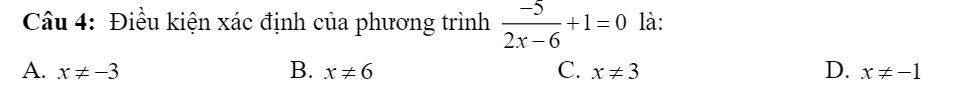
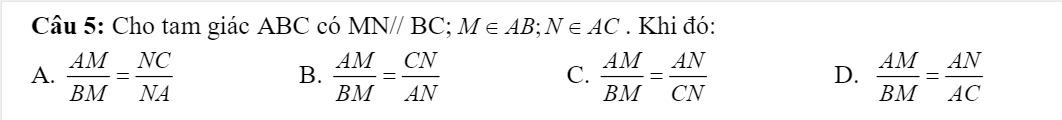 help mik vs
help mik vs 
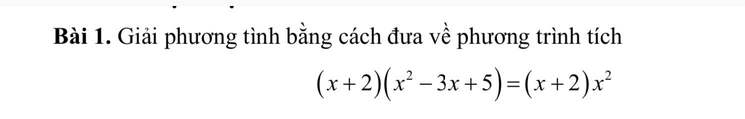


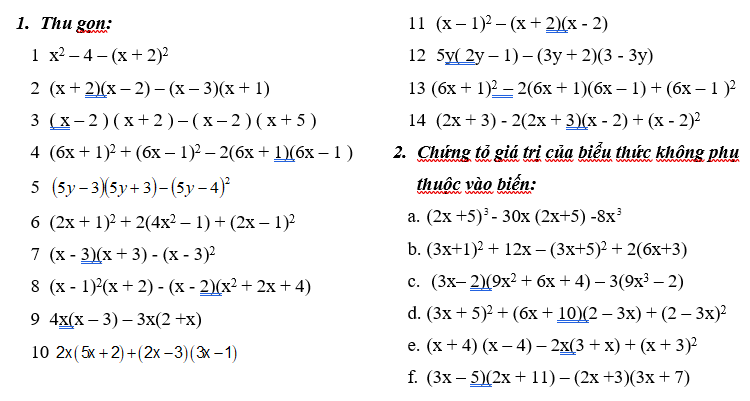
1d 2d 3d 4b 5a 6c