
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. ta có: AB = AE ( gt ) => tam giác ABE cân tại A
b.xét tam giác BAD và tam giác EAD có:
AB = AE ( gt )
góc BAD = góc EAD ( gt )
AD: cạnh chung
Vậy tam giác BAD = tam giác EAD ( c.g.c )
=> BD = ED ( 2 cạnh tương ứng )
a: Xét ΔABE có AB=AE
nên ΔABE cân tại A
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE
c: Ta có: ΔABD=ΔAED
nên \(\widehat{ABD}=\widehat{AED}=90^0\)
hay ED\(\perp\)AC
Ta có: BD=DE
mà DE<DC
nên BD<DC
d: Xét ΔADC có \(\widehat{DAC}=\widehat{C}\)
nên ΔADC cân tại D
=>DA=DC


a: Đặt a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7\cdot b^2k^2+3\cdot bk\cdot b}{11\cdot b^2k^2-8\cdot b^2}=\dfrac{b^2k\left(7k+3\right)}{b^2\left(11k^2-8\right)}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
\(\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7\cdot d^2k^2+3\cdot dk\cdot d}{11\cdot d^2k^2-8d^2}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
Do đó: \(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
c: \(\dfrac{3a+2c}{3b+2d}=\dfrac{3bk+2dk}{3b+2d}=k\)
\(\dfrac{a}{b}=\dfrac{bk}{b}=k\)
Do đó: \(\dfrac{a}{b}=\dfrac{3a+2c}{3b+2d}\)

\(2^x:1+2^x:2+...+2^x:49=2^{49}-1\)
\(2^x.1+2^x.\frac{1}{2}+...+2^x.\frac{1}{49}=2^{49}-1\)
\(2^x.\left(1+\frac{1}{2}+...+\frac{1}{49}\right)=2^{49}-1\)
Đặt: \(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\)
=> \(2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\)
=> \(2A-A=\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^{49}}\right)\)
=> \(A=1-\frac{1}{2^{49}}=\frac{2^{49}-1}{2^{49}}\)
\(2^{x-1}+2^{x-2}+2^{x-3}+...+2^{x-49}=2^{49}-1\)
<=> \(\frac{2^x}{2}+\frac{2^x}{2^2}+\frac{2^x}{2^3}+...+\frac{2^x}{2^{49}}=2^{49}-1\)
<=> \(2^x\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\right)=2^{49}-1\)
<=> \(2^x.\frac{2^{49}-1}{2^{49}}=2^{49}-1\)
<=> \(2^x=2^{49}\)
<=> x = 49.

V kế 3V - Nđ 3V;1,5V
V kế 5V- nguồn 3v,1,5v
V kế 9v - nguồn 3v,6v
V kế 15v - nguồn 12v

a/
\(x-y=\frac{a}{b}-\frac{c}{d}=\frac{ad-cb}{bd}=\frac{1}{bd}.\) (1)
\(y-z=\frac{c}{d}-\frac{e}{h}=\frac{ch-de}{dh}=\frac{1}{dh}\)(2)
+ Nếu d>0 => (1)>0 và (2)>0 => x>y; y>x => x>y>z
+ Nếu d<0 => (1)<0 và (2)<0 => x<y; y<z => x<y<z
b/
\(m-y=\frac{a+e}{b+h}-\frac{c}{d}=\frac{ad+de-cb-ch}{d\left(b+h\right)}=\frac{\left(ad-cb\right)-\left(ch-de\right)}{d\left(b+h\right)}=\frac{1-1}{d\left(b+h\right)}=0\)
=> m=y
+
cảm ơn bn nha Nguyễn Ngoc Anh Minh mk k cho bn r đó kb vs mk nha

Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2
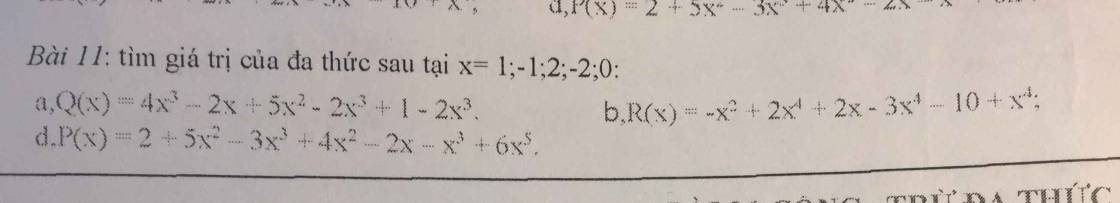


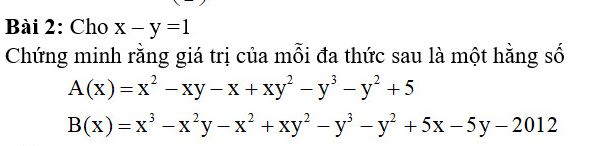
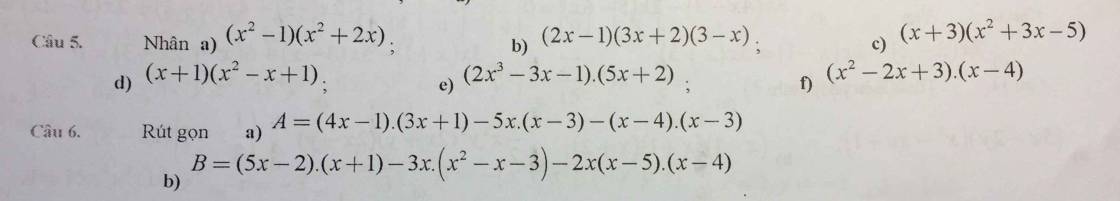
a: Q(x)=5x^2-2x+1
Q(1)=5-2+1=4
Q(-1)=5+2+1=8
Q(2)=5*2^2-2*2+1=5*4-4+1=16+1=17
Q(-2)=5*(-2)^2-2*(-2)+1=5*4+2*2+1=25
Q(0)=1
b: R(x)=-x^2+2x-10
R(1)=-1+2-10=1-10=-9
R(-1)=-(-1)^2+2(-1)-10=-1-2-10=-13
R(2)=-4+6-10=-8
R(-2)=-4-6-10=-20
R(0)=-10
d: P(x)=6x^5-4x^3+9x^2-2x+2
P(2)=6*2^5-4*2^3+9*2^2-2*2+2=194
P(-2)=6*(-2)^5-4*(-2)^3+9*(-2)^2-2*(-2)+2=-118
P(0)=2
P(1)=6-4+9-2+2=11
P(-1)=-6+4+9+2+2=11