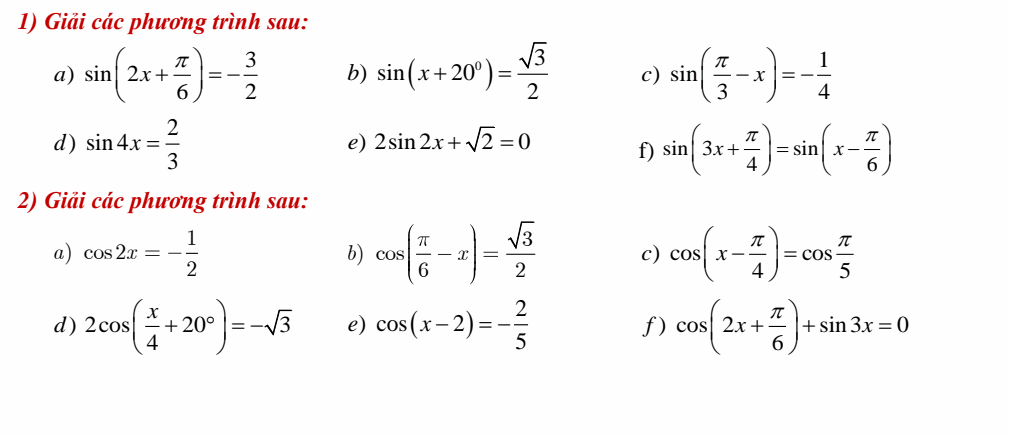K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
Vận tốc của chất điểm:
\(v\left(t\right)=s'\left(t\right)=3t^2-6t+9=3\left(t-1\right)^2+6\ge6\)
Dấu "=" xảy ra khi \(t-1=0\Rightarrow t=1s\)
DN
15 tháng 4 2022
Dạ em cảm ơn rất nhiều ạ, nhưng nếu được thầy có thể giải thích giúp em làm sao ra đc :S'(t) ạ ?
TG
0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
Tất cả \(k\in Z\)
1.
a. \(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
Đáp án trong đề bị sai
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cos7x-\dfrac{\sqrt{3}}{2}sin7x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(7x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{3\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}7x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\\7x+\dfrac{\pi}{3}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}7x=\dfrac{5\pi}{12}+k2\pi\\7x=-\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\\x=-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
Do \(\dfrac{2\pi}{5}\le x\le\dfrac{6\pi}{7}\Rightarrow\left[{}\begin{matrix}\dfrac{2\pi}{5}\le\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\\\dfrac{2\pi}{5}\le-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{143}{120}\le k\le\dfrac{67}{24}\\\dfrac{233}{120}\le k\le\dfrac{85}{24}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}k=1\\k=\left\{2;3\right\}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{53\pi}{84};\dfrac{5\pi}{12};\dfrac{59\pi}{84}\right\}\)
ND
1
12 tháng 10 2021
Giải thích các bước giải:
sin 2x=cos xsin 2x=cos x
⇔sin 2x=sin (π2−x)⇔sin 2x=sin (π2-x)
⇔⇔ ⎡⎢⎣2x=π2−x+k2π (k∈Z)2x=π−π2+x+k2π (k∈Z)[2x=π2−x+k2π (k∈Z)2x=π−π2+x+k2π (k∈Z)
⇔⇔ ⎡⎢⎣3x=π2+k2π (k∈Z)x=π2+k2π (k∈Z)[3x=π2+k2π (k∈Z)x=π2+k2π (k∈Z)
⇔⇔ ⎡⎢ ⎢⎣x=π6+k2π3 (k∈Z)x=π2+k2π (k∈Z)[x=π6+k2π3 (k∈Z)x=π2+k2π (k∈Z)
Vậy S={π6+k2π3 (k∈Z),π2+k2π (k∈Z)
PH
0
NT
1
23 tháng 12 2021
c)\(\left\{{}\begin{matrix}u_1+u_3=3\\u_1^2+u_3^2=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\\left(u_1+u_3\right)^2-2u_1u_3=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\u_1u_3=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}u_1=2\\u_3=1\end{matrix}\right.\\\left\{{}\begin{matrix}u_1=1\\u_3=2\end{matrix}\right.\end{matrix}\right.\)
Làm nốt (sử dụng công thức: \(u_n=u_1+\left(n-1\right)d\) để tìm được công sai
\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d\) để tính tổng 15 số hạng đầu)
d)\(\left\{{}\begin{matrix}u_1+u_2+u_3=14\\u_1u_2u_3=64\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_2-d+u_2+u_2+d=14\\\left(u_2-d\right)u_2\left(u_2+d\right)=64\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_2=\dfrac{14}{3}\\\left(u_2^2-d^2\right)u_2=64\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\dfrac{14}{3}=u_2=u_1+d\\d=\dfrac{2\sqrt{889}}{21}\end{matrix}\right.\\\left\{{}\begin{matrix}\dfrac{14}{3}=u_1+d\\d=\dfrac{-2\sqrt{889}}{21}\end{matrix}\right.\end{matrix}\right.\)
(Làm nốt,số xấu quá)
e)\(\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1^2+u_2^2+u_3^2=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1u_2u_3=\dfrac{21-\left(u_1+u_2+u_3\right)^2}{2}=-14\end{matrix}\right.\)
Làm như ý d)
SM
1
HP
8 tháng 9 2021
1.
c, \(sin\left(\dfrac{\pi}{3}-x\right)=-\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}-x=arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\\dfrac{\pi}{3}-x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\x=-\dfrac{2\pi}{3}+arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
d, \(sin4x=\dfrac{2}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=arcsin\dfrac{2}{3}+k2\pi\\4x=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\end{matrix}\right.\)
HP
8 tháng 9 2021
1.
e, \(2sin2x+\sqrt{2}=0\)
\(\Leftrightarrow sin2x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin2x=sin\left(-\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k\pi\\x=\dfrac{5\pi}{8}+k\pi\end{matrix}\right.\)
