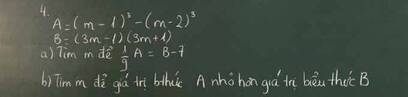K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 3 2022
a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
góc B chung
DO đó: ΔAHB\(\sim\)ΔCAB
Suy ra: AH/CA=AB/CB
hay \(AH\cdot BC=AB\cdot AC\)
b: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
nên ADHE là hình chữ nhật
c: BC=15cm
=>AH=7,2(cm)
mà AH=DE
nên DE=7,2(cm)
10 tháng 3 2022
a) Xét \(\Delta AHB\) và \(\Delta CAB:\)
\(\widehat{AHB}=\widehat{CAB}\left(=90^o\right).\\ \widehat{ABH}chung.\\ \Rightarrow\Delta AHB\sim\Delta CAB\left(g-g\right).\)
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{CB}.\\ \Rightarrow AH.CB=AB.AC.\)
b) Xét tứ giác DHEA:
\(\widehat{DAE}=90^o;\widehat{ADH}=90^o;\widehat{AEH}=90^o.\)
\(\Rightarrow\) Tứ giác DHEA là hình chữ nhật.
c) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=9^2+12^2.\\ \Rightarrow BC=15\left(cm\right).\)
Xét \(\Delta ABC\) vuông tại A; đường cao AH:
\(AH.BC=AB.AC\) (Hệ thức lượng).
\(\Rightarrow AH.15=9.12.\\ \Rightarrow AH=7,2\left(cm\right).\)
Mà \(AH=DE\) (Tứ giác DHEA là hình chữ nhật).
\(\Rightarrow AH=DE=7,2\left(cm\right).\)
2 tháng 12 2021
\(a,\left\{{}\begin{matrix}AM=MC\\AN=NB\end{matrix}\right.\Rightarrow MN\text{ là đtb }\Delta ABC\\ \Rightarrow MN\text{//}BC\Rightarrow MNBC\text{ là hình thang}\\ MN=\dfrac{1}{2}BC\Rightarrow BC=2MN=20\left(cm\right)\)
\(b,\text{Vì }M\text{ là trung điểm }AC,BD\text{ nên }ABCD\text{ là hbh}\\ c,\text{Vì }N\text{ là trung điểm }AB,CE\text{ nên }ACBE\text{ là hbh}\)
\(\Rightarrow AE\text{//}BC\\ \text{Mà }ABCD\text{ là hbh}\Rightarrow AD\text{//}BC\\ \Rightarrow AE\text{ trùng }AD\text{ hay }A,D,E\text{ thẳng hàng}\)
\(d,\left\{{}\begin{matrix}GI=IB\\GK=KC\end{matrix}\right.\Rightarrow IK\text{ là đtb }\Delta GBC\\ \Rightarrow IK\text{//}BC;IK=\dfrac{1}{2}BC\\ \text{Mà }MN\text{//}BC;MN=\dfrac{1}{2}BC\\ \Rightarrow IK\text{//}MN;IK=MN\\ \text{Vậy }MNIK\text{ là hbh}\)
DT
16 tháng 2 2022
b1:
AMF đồng dạng ABC
tỉ số : AM/AF = AB/AC
AM/MF = AB/BC
AF/FM = AC/CB
MFD đồng dạng CFD
tỉ số : MF/FD= FD/DC
FM/MD = DC/CF
FD/DM = DF/FC
AFB đồng dạng CFB
tỉ số : AB/ BF = BF/FC
AF/AB =BF/ BC
AF / FB = CF/BC
9 tháng 7 2021
a) Xét tứ giác AEHF có
\(\widehat{FAE}=90^0\)
\(\widehat{AEH}=90^0\)
\(\widehat{AFH}=90^0\)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ΔEHB vuông tại E(gt)
mà EN là đường trung tuyến ứng với cạnh huyền HB(N là trung điểm của HB)
nên \(EN=\dfrac{HB}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
1 tháng 8 2021
Gọi vận tốc của ô tô khách là \(x\left(x>0\right)\)
\(\Leftrightarrow\) Vận tốc của ô tô con là \(x+5\)
Quãng đường ô tô khách đi từ A đến lúc gặp nhau là : \(3x\left(km\right)\)
Quãng đường ô tô con đi từ B đến lúc gặp nhau là : \(3\left(x+5\right)\left(km\right)\)
Độ dài quãng AB là \(185km\)
\(\Leftrightarrow3x+3\left(x+5\right)=185\)
\(\Leftrightarrow6x+15=185\)
\(\Leftrightarrow x=\dfrac{85}{3}\)
Vậy....
MK
1
YN
20 tháng 6 2022
\(a)\)
\(A=\left(m-1\right)^3-\left(m-2\right)^3\)
\(=\left(m^3-3m^2+3m-1\right)-\left(m^3-6m^2+12m-8\right)\)
\(=m^3-3m^2+3m-1-m^3+6m^2-12m+8\)
\(=3m^2-9m+7\)
\(B=\left(3m-1\right)\left(3m+1\right)\)
\(=9m^2-1\)
\(\dfrac{1}{9}A=B-7\)
\(\Rightarrow\dfrac{1}{9}\left(3m^2-9m+7\right)=9m^2-1-7\)
\(\Rightarrow3m^2-9m+7=81m^2-72\)
\(\Rightarrow78m^2+9m-79=0\)
\(\Rightarrow m=\dfrac{-9\pm\sqrt{24729}}{156}\)
\(b)\)
\(A< B\)
\(\Rightarrow3m^2-9m+7< 9m^2-1\)
\(\Rightarrow6m^2+9m-8>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{-9+\sqrt{273}}{12}\\m< \dfrac{-9-\sqrt{273}}{12}\end{matrix}\right.\)
HL
0
