
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm



a) Ta có: \(A=\left(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
b) Thay \(x=7+4\sqrt{3}\) vào A, ta được:
\(A=\dfrac{2+\sqrt{3}+2}{2+\sqrt{3}-2}=\dfrac{4+\sqrt{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}+3}{3}\)
c) Ta có: \(M=\dfrac{x+5}{\sqrt{x}-2}:\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(=\dfrac{x+5}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow M\ge2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4\)
\(\Leftrightarrow M\ge2\cdot3-4=6-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=3\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1




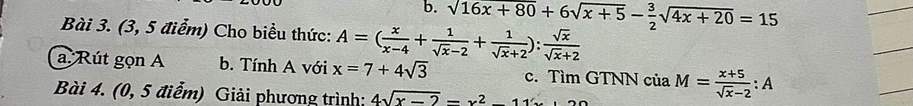 mn giúp em phần tìm gtnn vs ạ, em cần gấp
mn giúp em phần tìm gtnn vs ạ, em cần gấp