K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
25 tháng 7 2021
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
7 tháng 7 2021
a) Thay \(x=\dfrac{1}{4}\) vào Q, ta được:
\(Q=\dfrac{1}{\dfrac{1}{4}\cdot\dfrac{1}{2}+27}=\dfrac{1}{27+\dfrac{1}{8}}=\dfrac{8}{217}\)
b) Ta có: \(P=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{1}{2-\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-9+\sqrt{x}+3-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(P>\dfrac{1}{2}\) thì \(P-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\left(\sqrt{x}+3\right)}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)
LD
2
22 tháng 10 2021
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
22 tháng 10 2021
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
LA
1
22 tháng 7 2021
a) Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-2\sqrt{x}-1+2\left(\sqrt{x}+1\right)\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
B2
0
1
28 tháng 2 2022
a: Thay x=25 vào A, ta được:
\(A=\dfrac{5-1}{5+1}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: \(B=\dfrac{x-\sqrt{x}-x-2\sqrt{x}-1-2\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-5\sqrt{x}-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-5}{\sqrt{x}-1}\)
c: \(P=AB=\dfrac{-5}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{-5}{\sqrt{x}+1}\)
Để P<-1 thì P+1<0
\(\Rightarrow-5+\sqrt{x}+1< 0\)
\(\Leftrightarrow\sqrt{x}< 4\)
=>x<16
mà x là số nguyên lớn nhất
nên x=15
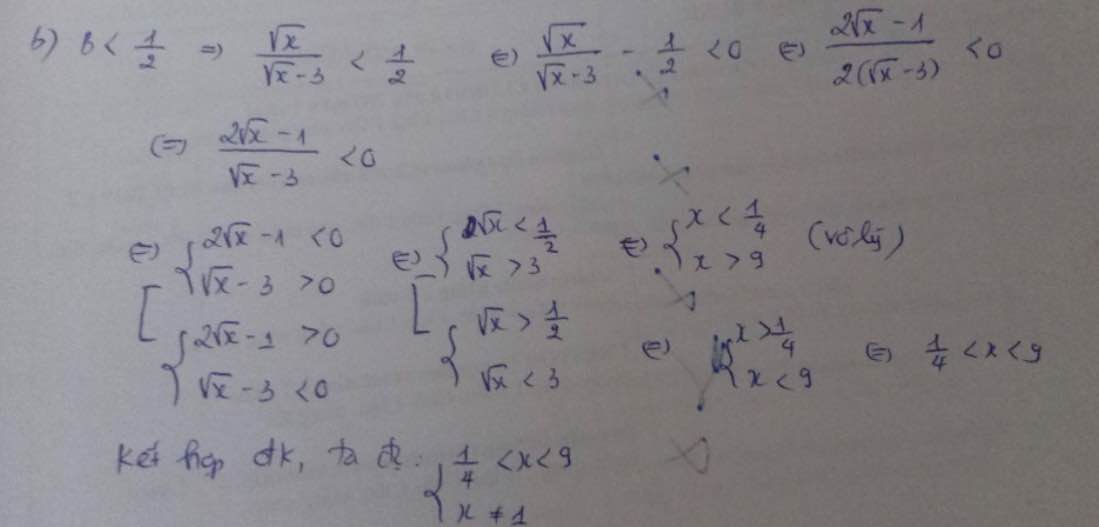
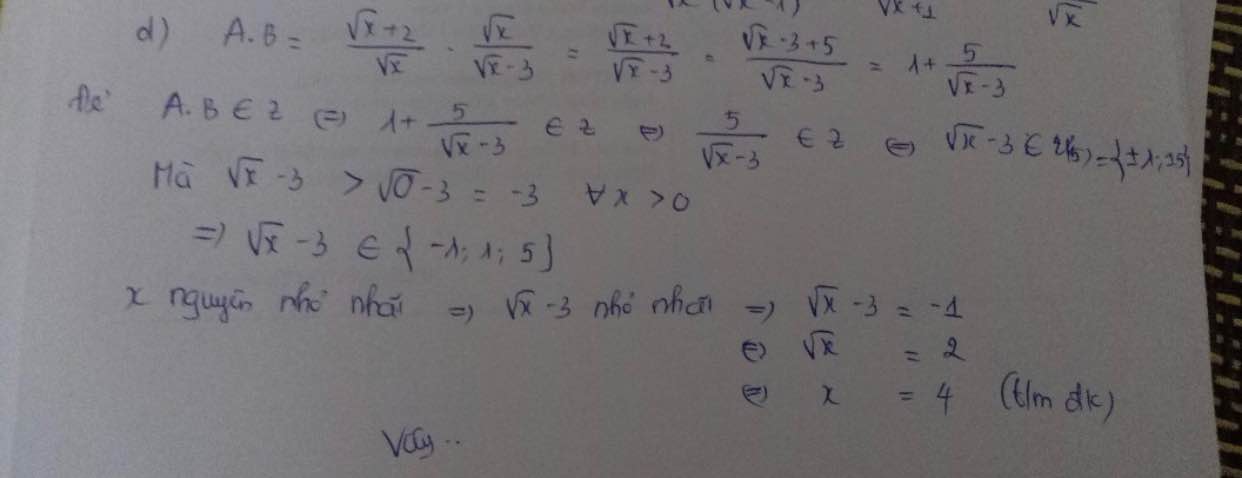
$A=x-3\sqrt{x}+1=(x-3\sqrt{x}+\frac{9}{4})-\frac{5}{4}$
$=(\sqrt{x}-\frac{3}{2})^2-\frac{5}{4}$
$\geq \frac{-5}{4}$
Vậy $A_{\min}=-\frac{5}{4}$. Giá trị này đạt tại $\sqrt{x}-\frac{3}{2}=0\Leftrightarrow x=\frac{9}{4}$
----------------
$B=\frac{3\sqrt{x}-1}{\sqrt{x}+2}=3-\frac{5}{\sqrt{x}+2}$
Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}+2\geq 2$
$\Rightarrow \frac{5}{\sqrt{x}+2}\leq \frac{5}{2}$
$\Rightarrow B\geq 3-\frac{5}{2}=\frac{1}{2}$
Vậy $B_{\min}=\frac{1}{2}$ khi $x=0$
$C=\frac{\sqrt{x}(\sqrt{x}+3)-3(\sqrt{x}+3)+19}{\sqrt{x}+3}$
$=\sqrt{x}-3+\frac{19}{\sqrt{x}+3}$
$=(\sqrt{x}+3)+\frac{19}{\sqrt{x}+3}-6$
$\geq 2\sqrt{19}-6$ theo BĐT Cô-si
Dấu "=" xảy ra khi $(\sqrt{x}+3)^2=19\Leftrightarrow x=28-6\sqrt{19}$