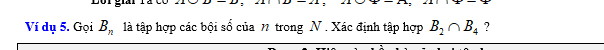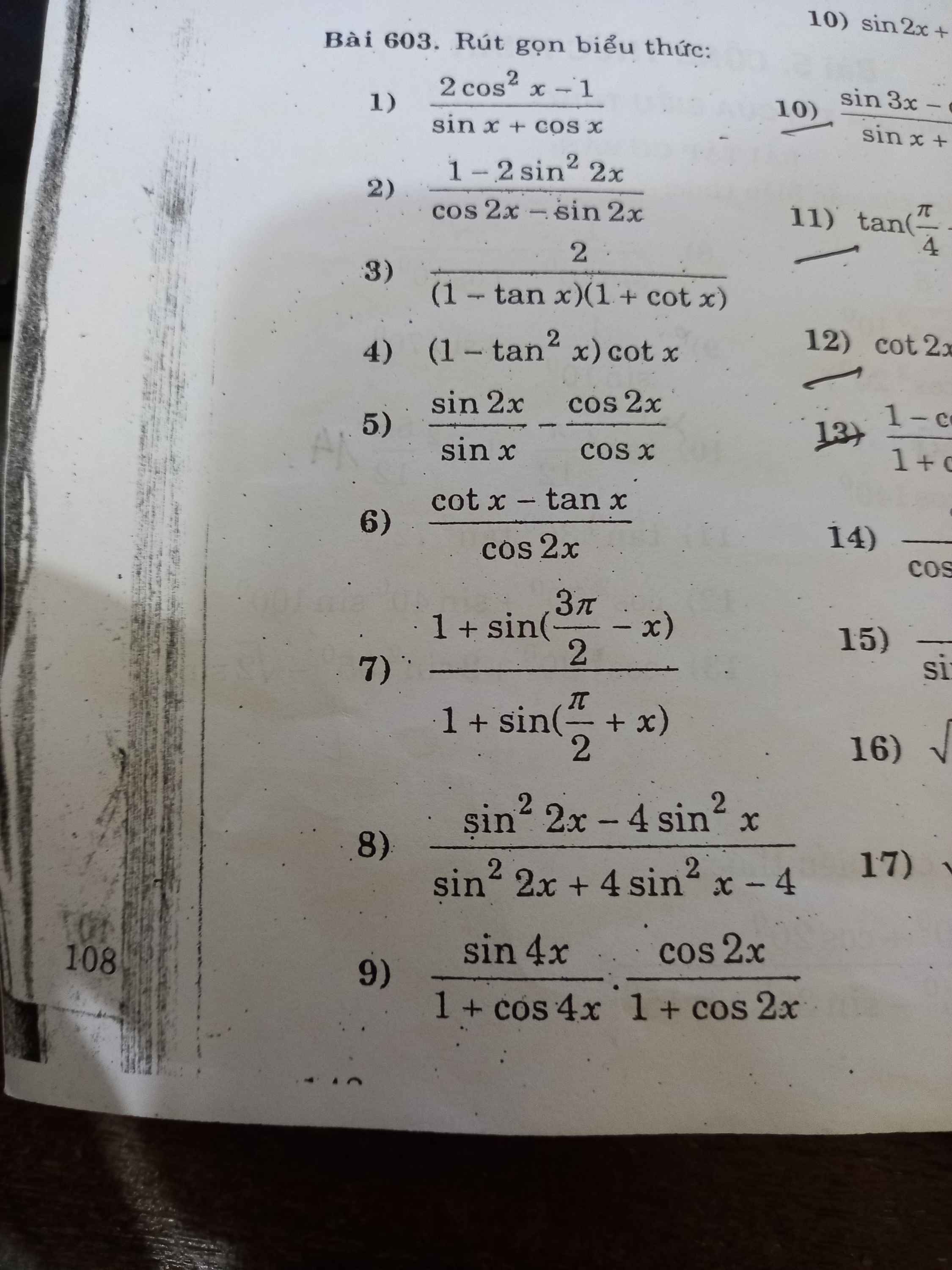CD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CD
0
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(B_2=\left\{x;x=2k,k\in N\right\}\)
\(B_4=\left\{x;x=4m,m\in N\right\}\)
Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)
\(\Rightarrow B_2\cap B_4=B_4\)
TP
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
2b.
\(Q=\dfrac{cosx}{sinx}+\dfrac{sinx}{1+cosx}=\dfrac{cosx\left(1+cosx\right)+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+1}{sinx\left(1+cosx\right)}=\dfrac{1}{sinx}\)
4b.
\(\Delta\) có 1 vtpt là (3;-4)
Gọi d là đường thẳng qua M và vuông góc \(\Delta\Rightarrow d\) nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x-4\right)+3\left(y+2\right)=0\Leftrightarrow4x+3y-10=0\)
H là giao điểm d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-4y+5=0\\4x+3y-10=0\end{matrix}\right.\) \(\Rightarrow H\left(1;2\right)\)
DT
0
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
10.
\(\dfrac{sin3x-cos3x}{sinx+cosx}=\dfrac{3sinx-4sin^3x-\left(4cos^3x-3cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(1-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{\left(sinx+cosx\right)\left(3-4+4sinx.cosx\right)}{sinx+cosx}\)
\(=-1+4sinx.cosx\)
\(=2sin2x-1\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
11.
\(tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{1+cos\left(\dfrac{\pi}{2}+x\right)}{sin\left(\dfrac{\pi}{2}+x\right)}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1+sin\left(-x\right)}{cos\left(-x\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1-sinx}{cosx}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}-2sin\dfrac{x}{2}cos\dfrac{x}{2}}{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)^2}{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)\left(cos\dfrac{x}{2}+sin\dfrac{x}{2}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\dfrac{x}{2}-sin\dfrac{x}{2}}{cos\dfrac{x}{2}+sin\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}{sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).cot\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\)
\(=1\)
29 tháng 6 2023
3:
\(=\dfrac{2}{1+cotx-tanx-1}=\dfrac{2}{cotx-tanx}\)
\(=2:\left(\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\right)=2:\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}\)
\(=\dfrac{sin2x}{cos2x}\)
=tan2x
4:
\(=\left(1-\dfrac{1}{cot^2x}\right)\cdot cotx=cotx-\dfrac{1}{cotx}=\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\)
\(=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}=\dfrac{cos2x}{\dfrac{1}{2}\cdot2\cdot sinx\cdot cosx}=\dfrac{cos2x}{sin2x}\cdot2\)
6:
\(=\dfrac{\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}}{cos2x}=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}:cos2x=\dfrac{1}{sinx\cdot cosx}\)
