Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Không mất tổng quát giả sử $C$ là góc nhọn.
\(\sin ^2A+\sin ^2B+\sin ^2C=\frac{1-\cos 2A}{2}+\frac{1-\cos 2B}{2}+\sin ^2C\)
\(=1+\sin ^2C-\frac{1}{2}(\cos 2A+\cos 2B)=1+\sin ^2C-\cos (A+B)\cos (A-B)\)
\(=1+\sin ^2C-\cos (180^0-C)\cos (A-B)\)
\(=1+\sin ^2C+\cos C\cos (A-B)=2-\cos ^2C+\cos C\cos (A-B)\)
\(\leq 2-\cos ^2C+\cos C\) với mọi $C$ nhọn
\(=\frac{9}{4}-(\cos C-\frac{1}{2})^2\leq \frac{9}{4}\)
Do đó mệnh đề đã cho đúng.

\(\left\{{}\begin{matrix}sinA=\dfrac{a}{2R}\\sinB=\dfrac{b}{2R}\\sinC=\dfrac{c}{2R}\end{matrix}\right.\) \(\Rightarrow sin^2A+sin^2B=\dfrac{a^2+b^2}{4R^2}=\dfrac{9+36}{4R^2}=\dfrac{45}{4R^2}\)
Trong khi đó \(3sin^2C=\dfrac{3.17}{4R^2}=\dfrac{51}{4R^2}\)
Đề bài sai

ta có A+B+C = ∏∏
nên C=∏∏ -(A+B)
nên ta có sin(A+B)=sinC , cos(A+B)=-cosC
ta có sin2A+sin2B+sin2C
=2sin(A+B)cos(A-B) + 2 sinCcosC
=2sinCcos(A-B)+2sinCcosC
=2sinC ( cos(A-B) + cosC)
=2sinC ( cos(A-B) - cos(A+B))
=2sinC.2sinAsinB
=4sinAsinBsinC
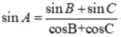
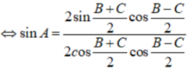
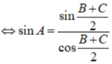
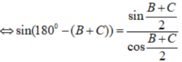
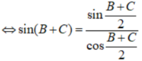
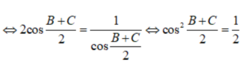
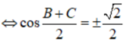
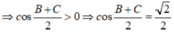
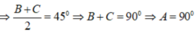
\(sin^2A+sin^2B+sin^2C=2\)
\(\Leftrightarrow sin^2A+\dfrac{1-cos2B}{2}+\dfrac{1-cos2C}{2}=2\)
\(\Leftrightarrow sin^2A-\dfrac{1}{2}\left(cos2B+cos2C\right)=1\)
\(\Leftrightarrow1-cos^2A-cos\left(B+C\right)cos\left(B-C\right)=1\)
\(\Leftrightarrow cos^2A+cos\left(B+C\right)cos\left(B-C\right)=0\)
\(\Leftrightarrow cos^2A-cosA.cos\left(B-C\right)=0\)
\(\Leftrightarrow cosA\left[cosA-cos\left(B-C\right)\right]=0\)
\(\Leftrightarrow cosA.sin\left(\dfrac{A+B-C}{2}\right)sin\left(\dfrac{A+C-B}{2}\right)=0\)
\(\Leftrightarrow cosA.sin\left(90^0-C\right)sin\left(90^0-B\right)=0\)
\(\Leftrightarrow cosA.cosB.cosC=0\)
\(\Leftrightarrow\left[{}\begin{matrix}A=90^0\\B=90^0\\C=90^0\end{matrix}\right.\) hay tam giác ABC vuông