K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
14
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
Tất cả k dưới đây đều là \(k\in Z\)
6.
\(\Leftrightarrow\sqrt{3}cot\left(3x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=cot\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow3x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{9}+\dfrac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
7.
\(\Leftrightarrow\sqrt{3}tan\left(3x-15^0\right)=-1\)
\(\Leftrightarrow tan\left(3x-15^0\right)=-\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow tan\left(3x-15^0\right)=tan\left(-30^0\right)\)
\(\Leftrightarrow3x-15^0=-30^0+k180^0\)
\(\Leftrightarrow3x=-15^0+k180^0\)
\(\Leftrightarrow x=-3^0+k60^0\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
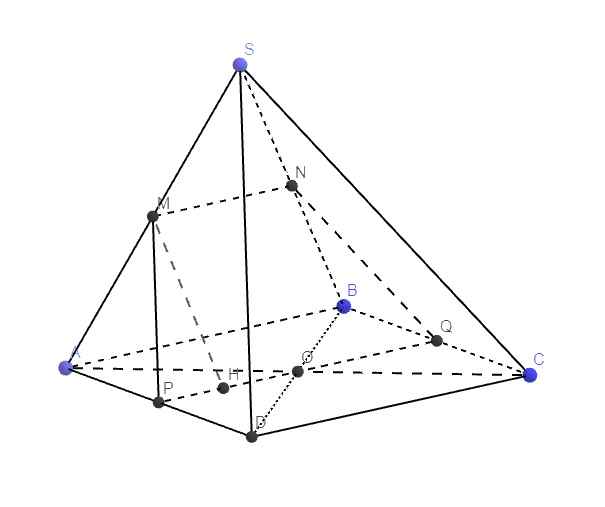
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
HP
24 tháng 8 2021
1.
Hàm số xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\cosx-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne k2\pi\end{matrix}\right.\Leftrightarrow x\ne k\pi\)
2.
Hàm số xác định khi:
\(cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
3.
\(cosx+1\ge0\Rightarrow\) Hàm số xác định với mọi x
4.
Hàm số xác định khi:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
5.
Hàm số xác định khi:
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
6.
Hàm số xác định khi:
\(cos3x-cosx\ne0\Leftrightarrow cos3x\ne cosx\Leftrightarrow3x\ne\pm x+k2\pi\Leftrightarrow\left[{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
1
E
14 tháng 12 2021
Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8
PN
0
HD
1
KB
1 tháng 5 2022
Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C
HP
10 tháng 9 2021
1.
a, \(sin2x-\sqrt{3}cos2x=-1\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=sin\left(-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{3\pi}{4}+k\pi\end{matrix}\right.\)
10 tháng 9 2021
Do tổng các hệ số thứ 1,2,3 là 46 nên ta có:\(C_n^0+C_n^1+C_n^2=46\)
\(\Leftrightarrow1+\dfrac{n!}{1!\left(n-1\right)!}+\dfrac{n!}{2!\left(n-2\right)!}=46\)
\(\Leftrightarrow1+n+\dfrac{\left(n-1\right)n}{2}=46\)
\(\Leftrightarrow n^2+n-90=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=9\\n=-10\left(loai\right)\end{matrix}\right.\)
Khai triển biểu thức: \(\left(x+\dfrac{1}{x}\right)^9\)
Hạng tử thứ k+1 trong biểu thức trên
\(\left(x+\dfrac{1}{x}\right)^9=C_9^{k+1}+\left(x^2\right)^{10-k}.\left(\dfrac{1}{x}\right)^{k+1}\)
đến đây mình chịu rùi hjhj b nào làm được giúp b kia với
2:
a: BC vuông góc SB; BC vuông góc AB
=>((SBC);(ABC))=góc ABS
tan ABS=SA/AB=căn 2
=>góc ABS=55 độ
b: AH vuông góc (SBC)
=>AH vuông góc HK
mà SB vuông góc AH
nên ((AHK);(SBA))=(SB;HK)=góc SHK
sin SHK=SK/SH
AC=AB*căn 2=a*căn 2
ΔSAC vuông cân tại A
=>SK=KA=KC=1/2*SC
=>SK=a
SA^2=SH*SB
SB=căn SA^2+AB^2=a*căn 3
=>SH=2a/căn 3
sin SHK=SK/SH=căn 3/2
=>góc SHK=60 độ
3:
a: d(A;(SBC))=AH=SA*AB/SC=a*căn 2/3
b: Kẻ BE vuông góc AC
=>E là trung điểm của AC
BE vuông góc AC;BE vuông góc SA
=>BE vuông góc (SAC)
=>d(B;(SAC))=BE=1/2*AC=a*căn 2/2
4:
a: (SB;(ABC))=góc SBA
tan SBA=căn 2
=>góc SBA=55 độ
b: (SC;(ABC))=góc SCA=45 độ
c: Kẻ HF vuông góc AB
=>HF//SA
=>HF vuông góc (ABC)
=>(AH;(ABC))=góc HAF=góc HAB=góc ASB
tan ASB=1/căn 2
=>góc ASB=35 độ