K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2021
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-\left(2x+1\right)+2x+1-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-\dfrac{4x^2}{\sqrt{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\left(-\dfrac{4}{\sqrt{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-4}{1+1}+\dfrac{12}{1+1+1}=2\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2021
\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{x+2017-\left(2015-x\right)}{\sqrt[3]{\left(x+2017\right)^2}+\sqrt[3]{\left(x+2017\right)\left(2015-x\right)}+\sqrt[3]{\left(2015-x\right)^2}}}{\dfrac{2000+x-\left(1998-x\right)}{\sqrt{2000+x}+\sqrt{1998-x}}}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\sqrt{2000+x}+\sqrt{1998-x}}{\sqrt[3]{\left(x+2017\right)^2}+\sqrt[3]{\left(x+2017\right)\left(2015-x\right)}+\sqrt[3]{\left(2015-x\right)^2}}\)
\(=\dfrac{\sqrt{1999}+\sqrt{1999}}{\sqrt[3]{2016^2}+\sqrt[3]{2016^2}+\sqrt[3]{2016^2}}=\dfrac{2\sqrt{1999}}{3.24\sqrt[3]{294}}=\dfrac{\sqrt{1999}}{36\sqrt[3]{294}}\)
\(\Rightarrow a+b=1999+294\)
25 tháng 8 2021
Phần bên trên giải thích rồi còn gì
n + n - 1 + n - 2 + n - 3 + .... + 1
Tổng của dãy số hơn kém 1 đơn vị lùi từ n về 1
T = (Số đầu - số cuối) . số số hạng rồi chia 2
tức là \(\dfrac{\left(n-1\right).n}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
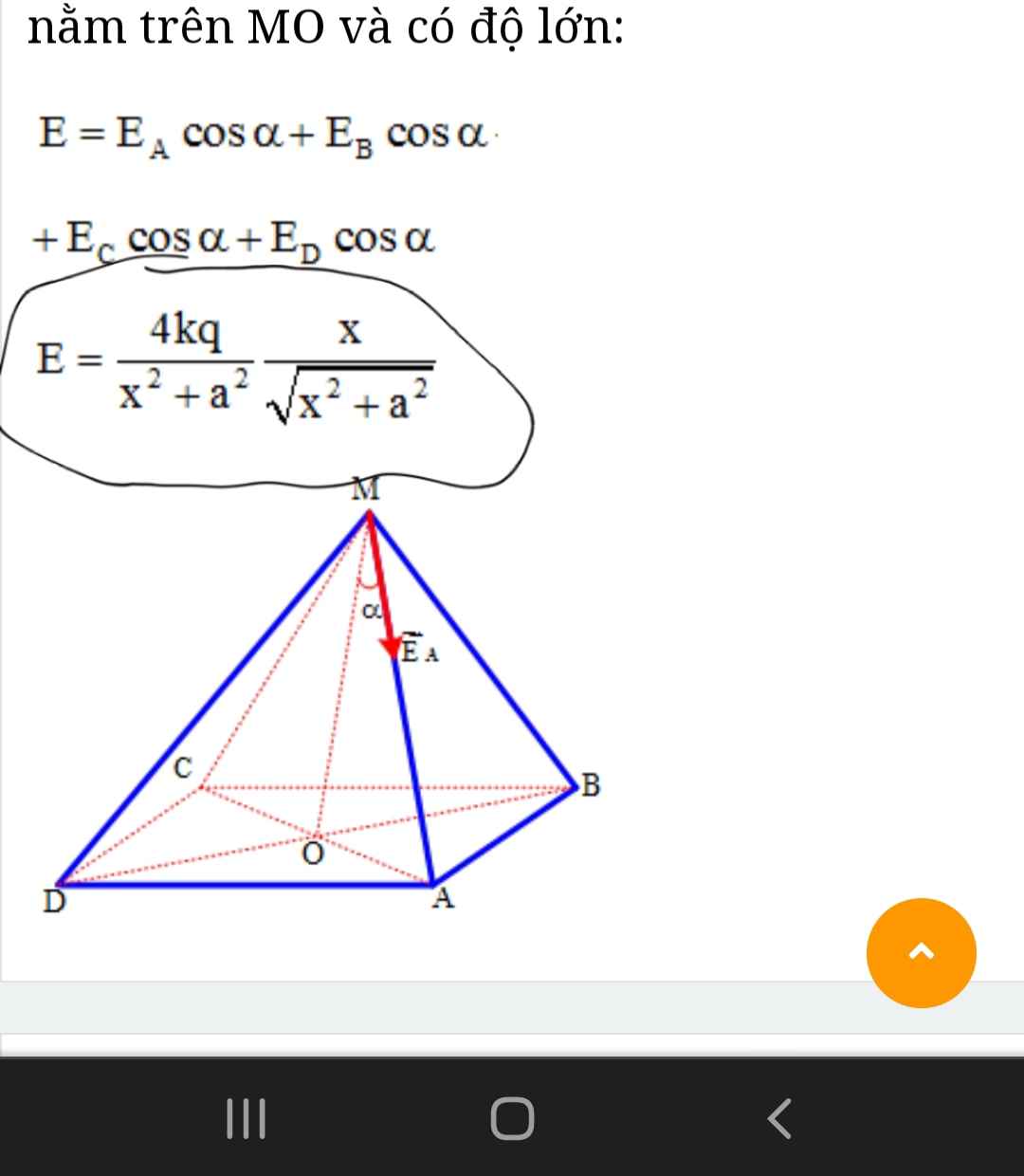
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)
DT
1
15 tháng 6 2023
38:
a: (SAB) và (SAC) cùng vuông góc (ABC)
(SAB) cắt (SAC)=SA
=>SA vuông góc (ABC)
b: SA vuông góc CH
CH vuông góc AB
=>CH vuông góc (SAB)
=>(SCH) vuông góc (SAB)
HT
9 tháng 3 2021
a/ \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt[3]{x^2-1}-2}{x-3}+\lim\limits_{x\rightarrow3}\dfrac{2-\sqrt[4]{1+5x}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^2-1-8}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{16-1-5x}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4.\sqrt[3]{1+5x}+8\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{-5\left(x-3\right)}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4\sqrt[3]{1+5x}+8\right)}\)
\(=\dfrac{3+3}{\sqrt[3]{\left(3^2-1\right)^2}+2.\sqrt[3]{3^2-1}+4}-\dfrac{5}{\sqrt[4]{\left(1+5.3\right)^3}+2\sqrt[3]{\left(1+5.3\right)^2}+4.\sqrt[3]{1+5.3}+8}=\dfrac{11}{32}\)
\(\Rightarrow a^2+b^2=1145\)
HT
9 tháng 3 2021
40/
\(L=\lim\limits_{x\rightarrow0}\dfrac{af\left(x\right)+b^n-b^n}{f\left(x\right)\left[\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+....+b^{n-1}\right]}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+...+b^{n-1}}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{b^{n-1}+b^{n-1}++...+b^{n-1}}=\dfrac{a}{nb^{n-1}}\)
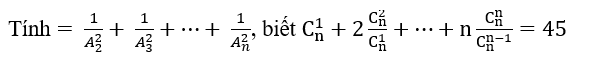
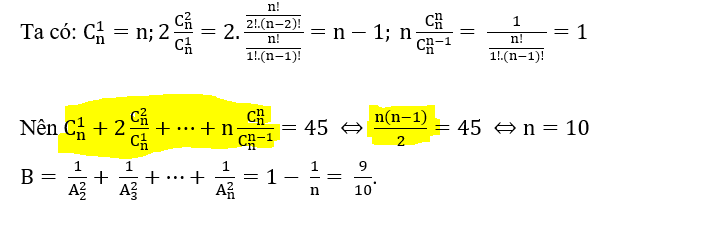
Bạn kiểm tra lại đề bài câu a, n=1 thì VT=1, VP=-1, nếu đề bài đúng thì vp phải là \(\dfrac{-\left(1\right)^{n-1}n\left(n+1\right)}{2}\)
\(n=1\Rightarrow VT=1=VP\)
Vậy mệnh đề đúng với n=1
Giả sử mệnh đề cũng đúng với \(n=k\left(k\in N\right)\), hay:
\(1^2-2^2+...+\left(-1\right)^{k-1}.k^2=\dfrac{\left(-1\right)^{k-1}.k.\left(k+1\right)}{2}\)
Ta cần chứng minh mệnh đề cũng đúng với \(n=k+1\) ,hay:
\(1^2-2^2+...+\left(-1\right)^{k-1}.k^2+\left(-1\right)^k.\left(k+1\right)^2=\dfrac{\left(-1\right)^k.\left(k+1\right)\left(k+2\right)}{2}\)
That vay:
\(VT=\dfrac{\left(-1\right)^{k-1}k\left(k+1\right)}{2}+\left(-1\right)^k.\left(k+1\right)^2=\dfrac{\left(-1\right)^{k-1}.k.\left(k+1\right)+2\left(-1\right)^k\left(k+1\right)^2}{2}\)
\(=\dfrac{\left(-1\right)^k\left(k+1\right)\left(-k+2k+2\right)}{2}=\dfrac{\left(-1\right)^k\left(k+1\right)\left(k+2\right)}{2}=VP\)
Vậy mệnh đề đúng với \(\forall n\in N\)
b/ \(n=7\Rightarrow VT=3^7=2187< 7!=5040\)
Vậy mệnh đề đúng với n=7
Giả sử mệnh đề đúng với \(n=k\left(k\in N;k\ge7\right)\),hay:
\(3^k\le k!\)
Ta cần chứng minh mệnh đề cũng đúng với \(n=k+1\) ,hay:
\(3^{k+1}\le\left(k+1\right)!\)
That vay:
\(3^k.3\le\left(k+1\right).k!\)
\(k>6\Rightarrow k+1>6\Rightarrow k+1>3\)
Ma \(3^k\le k!\)
\(\Rightarrow3^k.3\le\left(k+1\right).k!\Leftrightarrow3^{k+1}\le\left(k+1\right)!\)
Vậy mệnh đề đúng với \(\forall n\in N;n>6\)