K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 6 2023
a: góc ASB=1/2*180=90 độ=góc ABM
b: ON vuông góc AS
BS vuông góc SA
=>ON//BS
c: góc OIM+góc OBM=180 độ
=>OIMB nội tiếp
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
\(M=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
2. Ta có:
\(\sqrt{x}>0\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>0\) hay \(M>0\)
Lại có: \(M=\dfrac{\sqrt{x}+2-1}{\sqrt{x}+2}=1-\dfrac{1}{\sqrt{x}+2}< 1\)
\(\Rightarrow0< M< 1\Rightarrow M>M^2\)
10 tháng 7 2021
1) Ta có: \(M=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\sqrt{x}+2}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
3 tháng 10 2021
\(1,\\ a,=\dfrac{\sqrt{\left(\sqrt{a}-\sqrt{b}\right)^2}}{\sqrt{\left(\sqrt{a}-\sqrt{b}\right)}}=\sqrt{\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}}=\sqrt{\sqrt{a}-\sqrt{b}}\\ b,=\dfrac{\sqrt{\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}}{\sqrt{\sqrt{x}+\sqrt{3}}}\cdot\dfrac{\sqrt{3}}{\sqrt{\sqrt{x}-\sqrt{3}}}\\ =\sqrt{3}\\ c,=2y^2\cdot\dfrac{x^2}{\left|2y\right|}=\dfrac{2x^2y^2}{-2y}=-x^2y\\ d,=5xy\cdot\dfrac{\left|5x\right|}{y^2}=\dfrac{-25x^2y}{y^2}=\dfrac{-25x^2}{y}\)
3 tháng 10 2021
Bài 2:
a: Ta có: \(A=\left(3\sqrt{18}+2\sqrt{50}-4\sqrt{72}\right):8\sqrt{2}\)
\(=\left(9\sqrt{2}+10\sqrt{2}-24\sqrt{2}\right):8\sqrt{2}\)
\(=\dfrac{-5\sqrt{2}}{8\sqrt{2}}=-\dfrac{5}{8}\)
b: Ta có: \(B=\left(-4\sqrt{20}+5\sqrt{500}-3\sqrt{45}\right):\sqrt{5}\)
\(=\left(-8\sqrt{5}+50\sqrt{5}-9\sqrt{5}\right):\sqrt{5}\)
\(=49\)
KA
1
21 tháng 10 2021
Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
7 tháng 10 2021
a: \(x=\dfrac{6^2}{3}=12\left(cm\right)\)
\(y=\sqrt{6^2+12^2}=6\sqrt{5}\)
b: \(x=\sqrt{4\cdot9}=6\)
c: \(x=5\cdot\tan40^0\simeq4,2\left(cm\right)\)
23 tháng 12 2021
Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều
14 tháng 10 2021
\(a,ĐK:x\ge0;x\ne4\\ A=\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-2}=2\sqrt{x}+1\\ B=\dfrac{\left(x-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=x-1\\ b,M=A:B=\dfrac{2\sqrt{x}+1}{x-1}=\dfrac{2\left(\sqrt{x}+1\right)-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\\sqrt{x}+1\inƯ\left(1\right)=\left\{-1;1\right\}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\in\left\{0;2;3\right\}\left(\sqrt{x}\ge0\right)\\\sqrt{x}=0\left(\sqrt{x}\ge0\right)\end{matrix}\right.\Leftrightarrow x=0\)
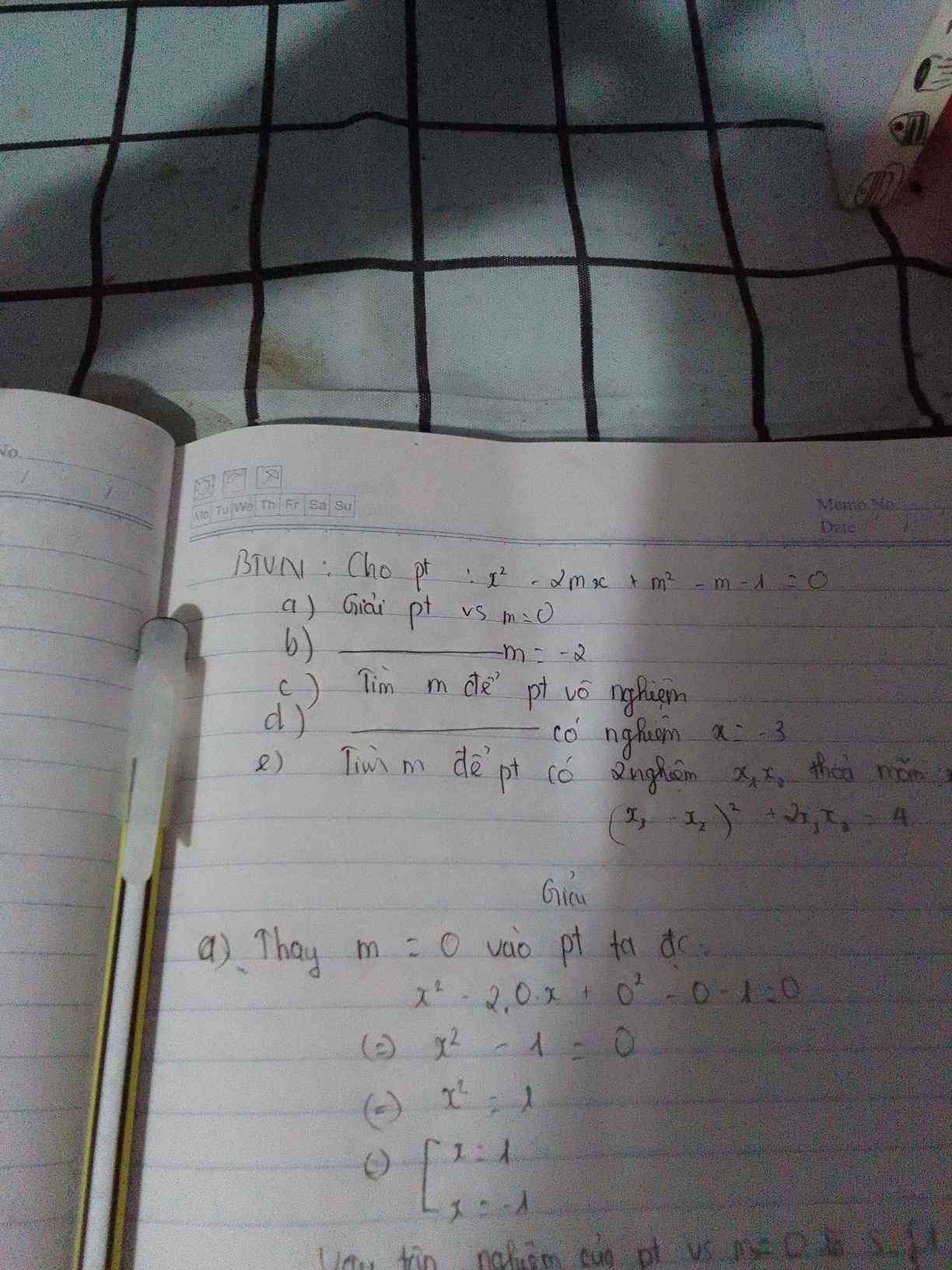
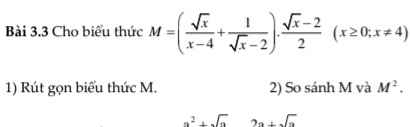
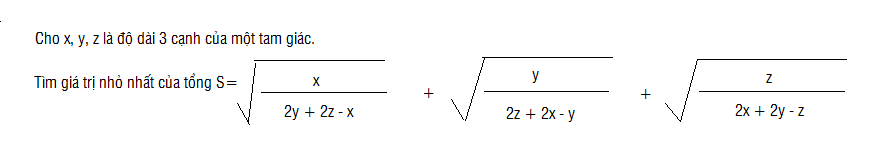
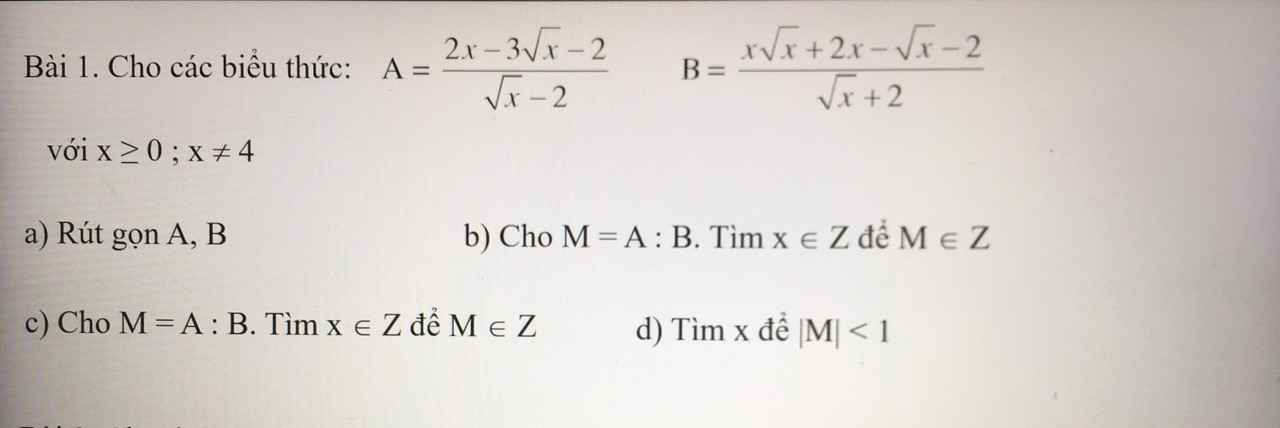
c: Để phương trình vô nghiệm thì \(\left(-2m\right)^2-4\left(m^2-m-1\right)< 0\)
=>4m+4<0
hay m<-1