T
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
NA
1
2 tháng 3 2023
a: ΔOBC cân tại O
ma OI là trung tuyến
nên OI vuông góc BC
=>góc OIA=90 độ
góc OIA=góc OMA=góc ONA=90 độ
=>O,I,M,A,N cùng thuộc đường tròn đường kính OA
Tâm là trung điểm của OA
R'=OA/2=R
b: Xét ΔAON vuông tại N có cos AON=ON/OA=1/2
nêngóc AON=60 độ
=>góc MON=120 độ
sđ cung MN=120 độ
c: Xét ΔAMB và ΔACM có
góc AMB=góc ACM
góc MAB chung
=>ΔAMB đồng dạng với ΔACM
=>AM/AC=AB/AM
=>AM^2=AB*AC
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
\(x^2+2x+2=\left(x+1\right)^2+1>0;\forall x\in R\)
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
\(3m+2=3+2m\Rightarrow m=1\)
TN
2 tháng 11 2021
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
x2+2x+2=(x+1)2+1>0;∀x∈Rx2+2x+2=(x+1)2+1>0;∀x∈R
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
3m+2=3+2m⇒m=1
A
1
AH
Akai Haruma
Giáo viên
28 tháng 5 2022
Lời giải:
Để pt có 2 nghiệm pb thì $\Delta'=1-(m-1)>0\Leftrightarrow m< 2$
Áp dụng hệ thức Viet:
$x_1+x_2=2$
$x_1x_2=m-1$
Khi đó:
$x_1^2+x_2^2-3x_1x_2=2m^2+|m-3|$
$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=2m^2+|m-3|$
$\Leftrightarrow 2^2-5(m-1)=2m^2+|m-3|$
$\Leftrightarrow 2m^2+5m+|m-3|-9=0$
$\Leftrightarrow 2m^2+5m+3-m-9=0$ (do $m< 2 < 3$)
$\Leftrightarrow 2m^2+4m-6=0$
$\Leftrightarrow m^2+2m-3=0$
$\Leftrightarrow (m-1)(m+3)=0$
$\Rightarrow m=1$ hoặc $m=-3$ (đều tm)
LB
1
25 tháng 8 2021
Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
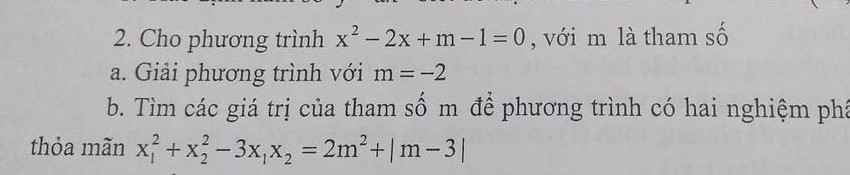
a.
ĐKXĐ: \(x\ge2\)
\(\dfrac{\sqrt{x}-\sqrt{x-1}}{\left(\sqrt{x}+\sqrt{x-1}\right)\left(\sqrt{x}-\sqrt{x-1}\right)}+\dfrac{\sqrt{x-1}-\sqrt{x-2}}{\left(\sqrt{x-1}+\sqrt{x-2}\right)\left(\sqrt{x-1}-\sqrt{x-2}\right)}=1\)
\(\Leftrightarrow\dfrac{\sqrt{x}-\sqrt{x-1}}{1}+\dfrac{\sqrt{x-1}-\sqrt{x-2}}{1}=1\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x-2}=1\)
\(\Leftrightarrow\sqrt{x}=1+\sqrt{x-2}\)
\(\Leftrightarrow x=1+x-2+2\sqrt{x-2}\)
\(\Leftrightarrow2\sqrt{x-2}=1\)
\(\Leftrightarrow x-2=\dfrac{1}{4}\)
\(\Rightarrow x=\dfrac{9}{4}\)
b
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}=\dfrac{x-1}{2}\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}=\dfrac{x-1}{2}\)
\(\Leftrightarrow\left|\sqrt{x-1}-1\right|+\left|\sqrt{x-1}+1\right|=\dfrac{x-1}{2}\)
Đặt \(\sqrt{x-1}=t\ge0\Rightarrow\left|t-1\right|+\left|t+1\right|=\dfrac{t^2}{2}\)
TH1: \(0\le t\le1\) pt trở thành:
\(1-t+t+1=\dfrac{t^2}{2}\Rightarrow t^2=4\)
\(\Rightarrow\left[{}\begin{matrix}t=2>1\left(ktm\right)\\t=-2< 0\left(ktm\right)\end{matrix}\right.\)
TH2: \(t>1\) pt trở thành:
\(t-1+t+1=\dfrac{t^2}{2}\Rightarrow t^2=2t\Rightarrow\left[{}\begin{matrix}t=0< 1\left(ktm\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}=2\Rightarrow x=5\)