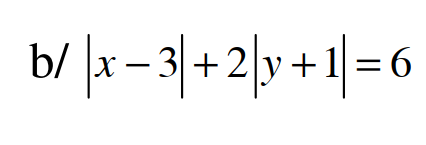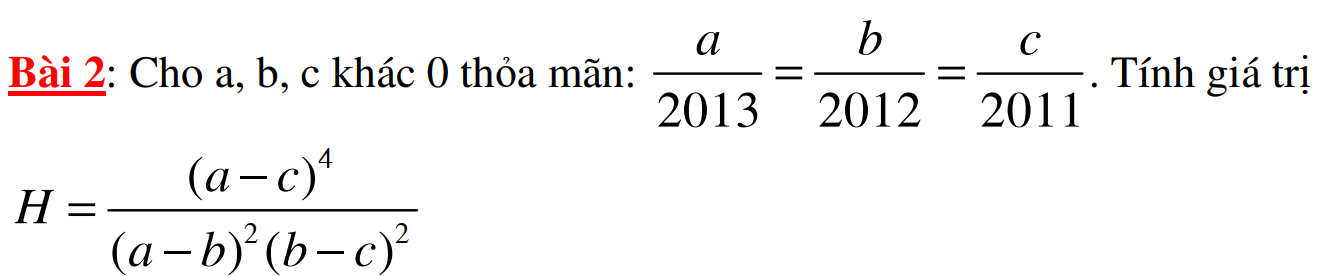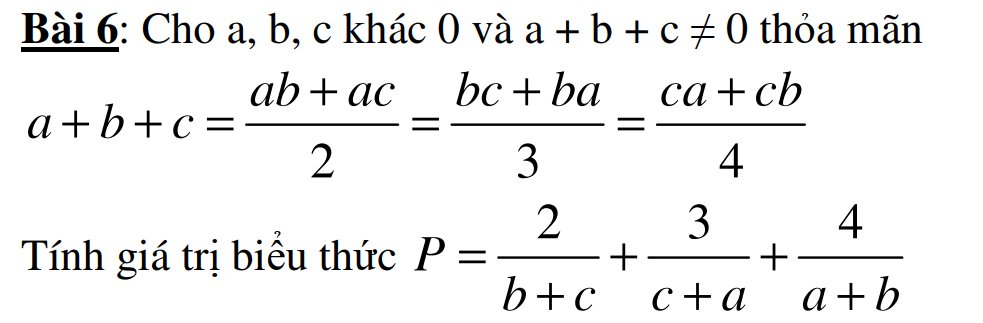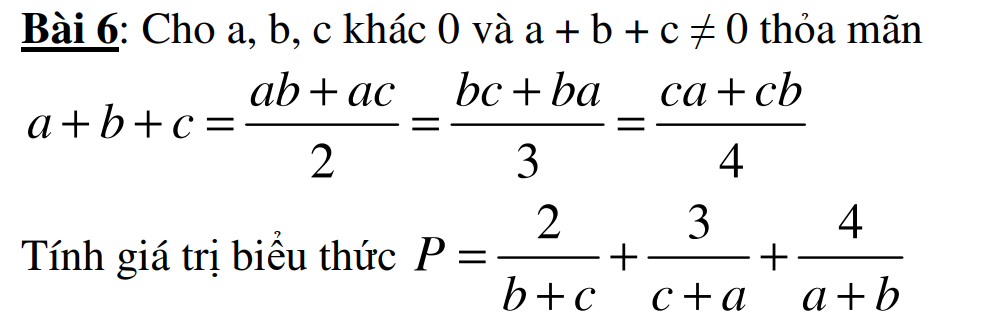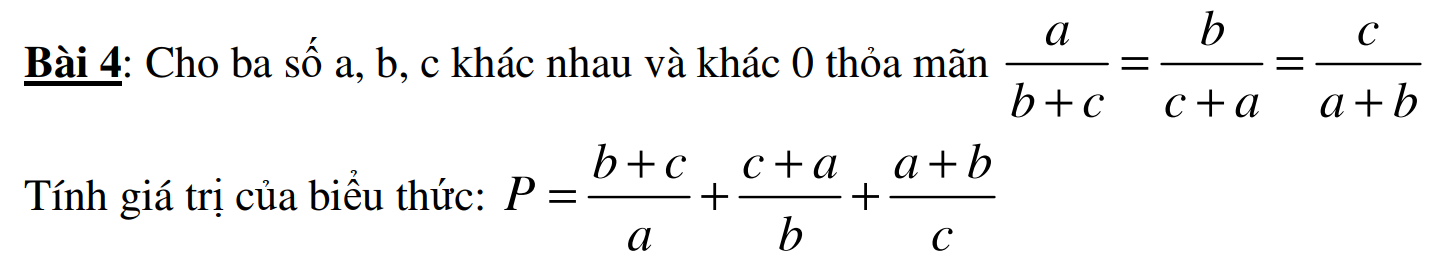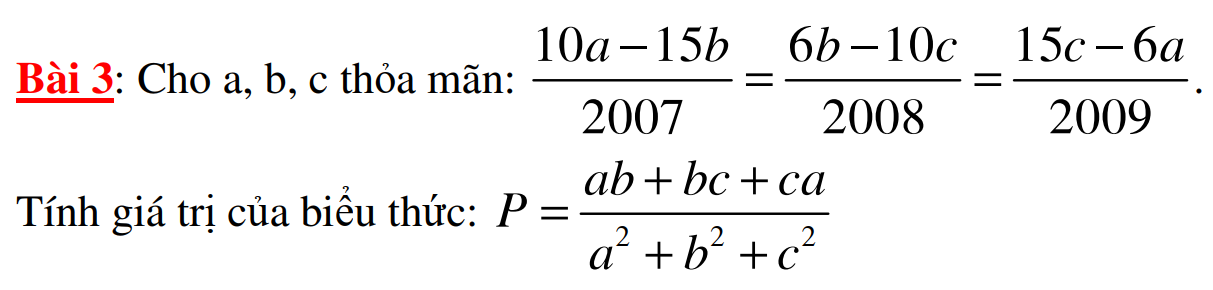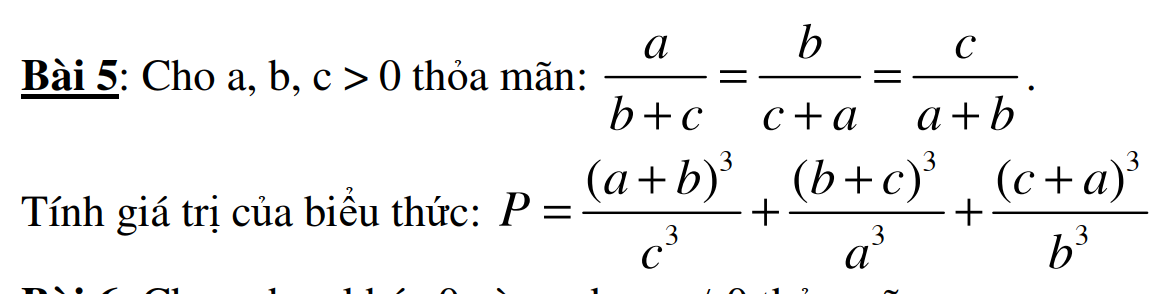K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
1
15 tháng 9 2021
Áp dụng t/c dãy tỉ số bằng nhau
\(\dfrac{a}{2013}=\dfrac{b}{2012}=\dfrac{c}{2011}=\dfrac{a-c}{2}=\dfrac{a-b}{1}=\dfrac{b-c}{1}\\ \Rightarrow a-c=2\left(a-b\right)=2\left(b-c\right)\)
\(\Rightarrow H=\dfrac{\left[2\left(a-b\right)\right]^4}{\left(a-b\right)^2\left(a-b\right)^2}=\dfrac{16\left(a-b\right)^4}{\left(a-b\right)^4}=16\)
NK
0
NK
0
NK
2
15 tháng 9 2021
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}b+c=2a\\c+a=2b\\a+b=2c\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{2a}{a}+\dfrac{2b}{b}+\dfrac{2c}{c}=2+2+2=6\)
S
15 tháng 9 2021
P=
\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{a}{b+c}.\left(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\right):\left(\dfrac{a}{b+c}\right)=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{a}{b+c}+\dfrac{a+b}{c}.\dfrac{a}{b+c}\right):\dfrac{a}{b+c}=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{b}{c+a}+\dfrac{a+b}{c}.\dfrac{c}{a+b}\right):\dfrac{a}{b+c}=\left(1+1+1\right):\dfrac{a}{b+c}=3.\dfrac{b+c}{a}=\dfrac{3b+3c}{a}\)
NK
1
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
Bổ sung điều kiện $a,b,c$ không thể đồng thời bằng $0$
Từ đkđb suy ra:
\(\frac{6(10a-15b)}{2007.6}=\frac{15(6b-10c)}{15.2008}=\frac{10(15c-6a)}{10.2009}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{6(10a-15b)}{2007.6}=\frac{15(6b-10c)}{15.2008}=\frac{10(15c-6a)}{10.2009}=\frac{6(10a-15b)+15(6b-10c)+10(15c-6a)}{2007.6+15.2008+10.2009}=0\)
\(\Rightarrow 10a-15b=6b-10c=15c-6a=0\)
\(\Leftrightarrow 10a=15b; 6b=10c; 15c=6a\Leftrightarrow \frac{a}{15}=\frac{b}{10}=\frac{c}{6}\)
Đặt $\frac{a}{15}=\frac{b}{10}=\frac{c}{6}=k$ thì: $a=15k, b=10k, c=6k$
Vì $a,b,c$ không thể đồng thời bằng $0$ nên $k\neq 0$
Khi đó:
$P=\frac{15k.10k+10k.6k+15k.6k}{(15k)^2+(10k)^2+(6k)^2}$
$=\frac{300k^2}{361k^2}=\frac{300}{361}$
NK
1
15 tháng 9 2021
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}2a=b+c\\2b=a+c\\2c=a+b\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{\left(a+b\right)^3}{c^3}+\dfrac{\left(b+c\right)^3}{a^3}+\dfrac{\left(c+a\right)^3}{b^3}=\left(\dfrac{a+b}{c}\right)^3+\left(\dfrac{b+c}{a}\right)^3+\left(\dfrac{c+a}{b}\right)^3=\left(\dfrac{2c}{c}\right)^3+\left(\dfrac{2a}{a}\right)^3+\left(\dfrac{2b}{b}\right)^3=2^3+2^3+2^3=24\)
NK
0
TA
1
8 tháng 8 2021
Đề bài thiếu bạn nhé, có lẽ là x và y là các số nguyên.
TA
2
NM
Nguyễn Minh Quang
Giáo viên
10 tháng 8 2021
ta có \(\left(x-4\right)\left(6-x\right)\le\left(\frac{x-4+6-x}{2}\right)^2=1\) (bất đẳng thức cauchy)
mà \(\left|y+1\right|\ge0\Rightarrow\left|y+1\right|+2\ge2>1\)
Vậy phương trình trên vô nghiệm
